双变量分析检验两个变量是如何相互关联的。最普通的双变量统计是双变量相关系数(经常被简称为“相关系数”),一个介于-1与1之间的值,表示了两个变量之间的相关强度。假设我们希望研究年龄如何跟自尊相关,以20个调查对象为样本,比如随着年龄的增长,自尊是会增加,减少,还是不变。如果自尊增加,那么我们得到这两个变量间的正相关关系;如果自尊减少,我们得到负相关关系;如果保持不变,我们得到零相关关系。为了计算相关系数的值,考虑图表 14.3的假设数据集。
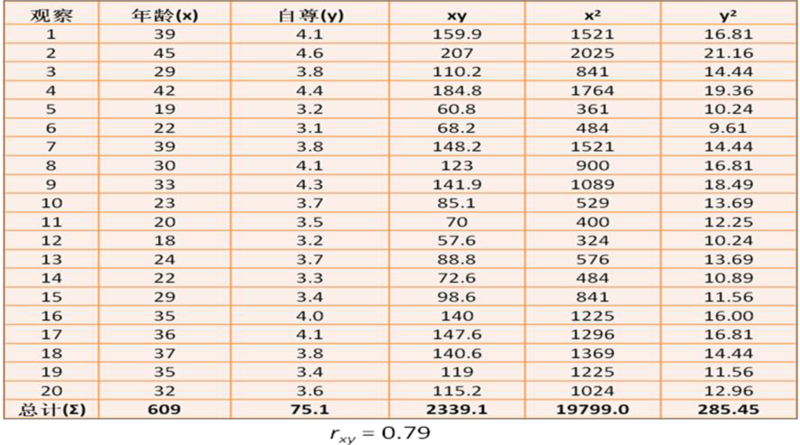
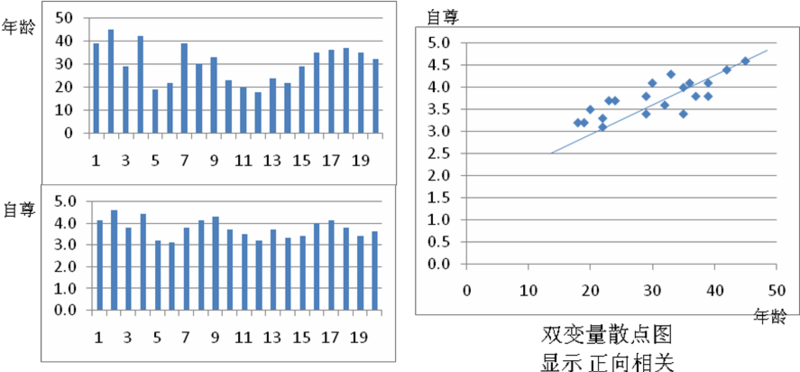
这个数据集中的两个变量是年龄(x)和自尊(y)。年龄是一个定比变量,而自尊是从多要素自尊量表计算的平均得分而来的,运用七点式李克特量表,从“强烈不同意”到“强烈同意”变动。每个变量的直方图显示在图表 14.4左列。计算双变量相关系数的方程是:
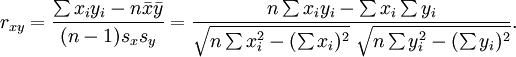
rxy是相关系数,x和y是变量x和y的样本均值,sx和sy是变量x和y的标准差。如图表 14.3所示,手工计算年龄和自尊之间的相关系数是0.79。这个数字表明了年龄和自尊之间强烈正相关。即自尊倾向于随着年龄的增长而增强,随着年龄的减 小而减弱。这样的模式也可以从比较图表 14.4中的年龄和自尊的直方图看得出,两个直方图的顶点大致相互紧随。图表 14.4的纵轴表示真实的观测值而不是观测值的频数(如图表 14.1所示)。因此,这不是频数分布而是直方图。图表 14.4的右侧是双变量的散点图,纵轴表示自尊,横轴表示年龄。这个图粗略地聚集成了 一个上倾的斜线(即正斜率)。如果两个变量是负相关,散点图应该是向下倾斜的(负斜率),表明年龄的增长与自尊的减弱相关,反之亦然。如果两个变量不相 关,散点图将接近于一条水平线(零斜率),表明年龄的增长与自尊非系统相关。
在计算了双变量相关性后,研究者通常比较有兴趣知道相关性是否显著(即一个真正的)或是仅仅偶然引起的。回答这样一个问题需要检验如下假设:
H0:r=0
H1:r≠0
H0被称为原假设,H1被称为备择假设(有时也表示为Ha)或我们真正想要检验的假设(即相关系数是否异于0)。尽管他们可能看起来像两个假设,H0和H1联合代表了一个单一的假设,因为他们彼此相反。也要注意到H1是非方向性的假设,因为它没有具体说r是大于还是小于0。方向性假设具体为:H0:r≤0;H1:r>0(如果我们检验正相关)。方向性假设的显著性检验用单尾t检验做,而非方向性检验用双尾t检验做。
在统计检验中,备择假设不能被直接或者推定证明。然而,它可以通过在特定概率水平下显著拒绝原假设而被间接证明。统计检验经常是概率性的,因为我们从来不确定基于样本数据的推断是否适用于总体,因为我们的样本从来不等于总体。纯属巧合的统计推断的概率被称为p值。p值是跟显著性水平(α)相对的。α表示我们愿意接受推断是不正确的最大风险水平。对于大多数统计分析,α被设定为0.05。p值小于α=0.05表明我们有足够的统计证据拒绝原假设,因此,间接接受了备择假设。如果p>0.05,那么我们没有充足的证据拒绝原假设或接受备择假设。
检验上述假设最简单的方法是在统计表格中查阅r的临界值。统计表格在任何标准的统计教科书或互联网上(大多数软件程序也执行显著性测试)都可以得到。r的临界值依赖于我们所要求的显著性水平(α=0.05),自由度(df)以及要求的检验是单尾检验还是双尾检验。自由度是指在统计的任何计算中可以自由变动的值的数量。在相关系数中,自由度等于n–2。如在表14.1中,自由度是20–2=18。对于单尾检验和双尾检验有两种不同的统计表格。在双尾检验中,对于α=0.05、df=18,r的临界值是0.44。要是我们计算的0.79的相关性显著,r必须大于临界值0.44或小于-0.44。由于我们计算的0.79大于0.44,可以推论出在我们的数据集中,年龄和自尊有显著的相关性。也就是说相关性是偶然性的概率小于5%。因此,我们可以拒绝r≤0的原假设,间接表明了r>0的备择假设是可能正确的。
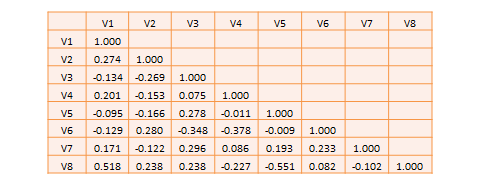
大多数研究涉及多于两个变量。如果有n个变量,那么在这n个变量中,我们将共有n*(n-1)/2个相关系数。此类相关系数通过如SPSS样的软件程序可以轻易地计算出,而不是相关系数公式(如图表 14.3)手工计算,并且以相关系数矩阵的形式列示,如图表 14.5所示。一个相关系数矩阵是这样一个矩阵:在第一行和第一列列示变量名称,并在矩阵合适的单元格中描述一组变量间的双变量相系数。这个矩阵的主对角线(从左上角到右下角)的值一般为1,因为任何变量都跟它自身完全相关。而且,由于相关性是非方向性的,变量V1和V2间的相关系数与V2和V1间的相关系数是一样的。因此,下三角矩阵(主对角线以下的值)是上三角矩阵(主对角线以上的值)的一面镜子。如此,为了简洁,我们便常常只列示出下三角矩阵。如果相关性包括以等距尺度计量的变量,那么相关系数的具体类型被称为皮尔逊积差相关系数。
列示双变量数据的另一种有用的方式是交叉表格(常简称为交叉表,有时也被更正式地称为列联表)。交叉表是一个描述两种及两种以上的定类或分类变量的所有组合频数(或百分比)的表格。例如,我们假设有20个学生样本的关于性别和分数的观测值,如图表 14.4。姓名是一个定类变量(女/男),分数是一个有三个等级(A/B/C)的分类变量。在一个2x3的矩阵中,数据的简单列联表列示了性别和分数间的联合分布(即每个等级每个性别的学生有多少个,以行频数计数或百分比表示)。这个 矩阵将帮助我们看清A、B、C三个等级的分数是否均匀分布在男生和女生中。图表 14.6中的交叉表数据表明A级分数分布偏向于女生:样本有10个男生10个 女生,5个女生拿到了A,而仅一个男生拿到A。相反,C级分布偏向于男生:3个男生拿到C,而仅一个女生拿到C。然而,B级的分布是有点统一的,6个男生 和5个女生拿到B。表格中的最后一行和最后一列被称为边际总数,因为他们表示每类的总数并列示在表格的边上。
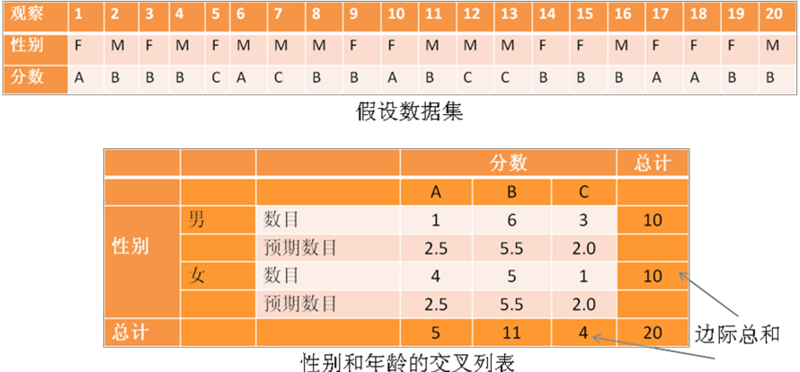
尽管我们可以看到图表 14.6中男生和女生的分数分布有明显不同的模式,这个模式是否是真正的或“统计显著”呢?换句话说,以上的频数计数与纯属巧合的预期是否不同呢?为了回答这个问题,我们应该在2x3的交叉表矩阵的每个单元格中计算观测者的预期数。这个可以通过乘以边际列总数和边际行总数再除以总观测值的数量计算得到。例如,男生/A级的单元格,预期计数=5*10/20=2.5。换而言之,我们预期有2.5个男生得到A,但是实际上只有一个男生拿到A。预期值和真实值之间的差异是否显著可以通过卡方检验来检验。卡方统计量是计算所有单元格的观测值和预期值均值的差异。然后我们可以将这个数与临界值相比较,临界值是通过期望概率水平(p<0.05)和自由度确定。自由度即(m-1)*(n-1),m和n分别表示行和列的数量。任何教科书中标准卡方表格中,对于p=0.05和df=2,临界的卡方的值为5.99。基于我们的观测数据计算的卡方值是1.00,小于临界值。由此,我们一定可以推论出观察到的分数模式与纯属巧合的预期不是统计上显著区别的。
- 瀏覽次數:14372






