A computer system is a state machine that is composed of many individual circuitries driven by one or more internal clocks. These internal clocks are usually described by their frequency, or clock rate. The term MHz is a combination of two acronyms, M and Hz:
M, or mega -- a quantity equals to a million, or 106.
Hz, or Hertz -- the number of cycles per second.
Therefore, a 500 MHz clock is equal to 500 million cycles per second, or 5 × 108 cycles per second. Over the years, much confusion has been cast over the acronyms for the quantities such as: kilo, mega, giga, tera, peta, and so on. Depending on the context, the acronyms may refer to two different quantities: a kilohertz usually means 1,000 Hertz, and a megahertz usually means 1,000,000 Hertz.
| Kilo (K) | = 1 × 103 or 1,000 |
| Mega (M) | = 1 × 106 or 1,000,000 |
| Giga (G) | = 1 × 109 or 1,000,000,000 |
| Tera (T) | = 1 × 1012 or 1,000,000,000,000 |
| Peta (P) | = 1 × 1015 or 1,000,000,000,000,000 |
When we compile a software program written in high-level languages like C++ or FORTRAN, the compiler translates the software program into an ordered collection of machine-understandable instructions. The processor will then execute these instructions through a number of cycles. Let's consider the following example.
Example
The example you just seen is an over simplification of what is really going on under the hood of a computer system. In reality, virtually every computer system today is installed with a multi-programming-enabled operating system. Therefore, the execution time of a user program may include other activities such as waiting for an I/O event or running other jobs. Sometimes, we refer to the execution time of a program as the wall-clock time, which represents the total time elapsed since the start of the program. The time period that the CPU spends on executing user code is called user time or CPU time; and the time spent by the processor on other activities is called system time. Hence:
|
Execution time |
= Wall-clock time |
We are only interested in the performance results measured from an unloaded system -- that means the operating system is not busy multiplexing other jobs onto the processor (i.e. minimize the system time). There are three major components in the previous example: the number of instructions in a program, the number of CPU cycles per instruction, and the length of each CPU cycle.
We can summarize these variables into the following equation, called the CPU performance equation:

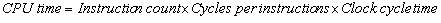

Note that instruction count (IC) refers to the total number of instructions executed by the processor, and that cycles per instruction (CPI) is the average number of cycles per instruction.
Definitions
Instruction count (IC): total number of instructions executed by the processor.
Cycles per instruction (CPI): the average number of cycles per instruction.
The CPU performance equation you've just learned gives us some clues about how we could improve the performance of a computer system:
- Reduce the number of instructions executed by a program; or
- Reduce the number of cycles per instruction; or
- Reduce the time of each CPU cycle; or
- Any combination of the above.
However, it is not easy to improve the system performance by reducing one variable without affecting others:
- The number of instructions to be executed by a program is determined by the instruction set architecture as well as the compiler technology. (This may or may not have anything to do with the program size. Sometimes, a small program size may have a large instruction count (e.g. a loop). On the other hand, expanding a loop many times will lead to a large program, but the number of instructions executed will decrease because of the reduction in the loop overhead);
- The number of cycles per instruction is dependent on the instruction set architecture and the machine organization; and
- The CPU cycle time depends on the hardware technology and the machine organization.
For example, it is very easy to create an instruction set that can reduce the total number of instructions in a program (e.g. the x86 instruction set versus the RISC instruction set). However, this change is likely to cause the total number of cycles per instruction to increase, off-setting the enhancement from the reduced instruction count.
In addition to the CPU performance equation, there are other metrics and standards that have been used for decades to compare the performance of computer systems. We'll review several of them in this section.
MOPS -- Millions of Operations Per Second
Sometimes we interchange MOPS with the term MIPS -- Millions of Instructions Per Second. MOPS refers to the total number of operations (instructions) executed, or that a processor can execute in a second. For example, a processor with a 500 MHz clock, with a CPI of 1, is capable of delivering 500 MOPS. This metric is somewhat misleading because the instruction count depends on the instruction set architecture, which is processor dependent. A FORTRAN program compiled on machine X may have a totally different instruction count on machine Y, which leads to inaccurate performance conclusions if MIPS is the only metric used in the comparison.
MFLOPS -- Millions of FLoating-point Operations Per Second
The majority of scientific applications run on computers today are packed with many floating-point calculations. MFLOPS measures the performance of the computer system to execute floating-point operations such as add, subtract, multiply and so on. MFLOPS refers to the total number of floating-point operations executed in millions per second. With today's high-powered processors, we often pronounce MFLOPS as Mega-FLOPS. Thus, GFLOPS, or Giga-FLOPS is 1,000 times more than MFLOPS; and TFLOPS, or Tera-FLOPS is 1,000,000 times more than a MFLOPS.
So, you might ask, who needs TFLOPS? Applications such as weather prediction will not be useful if the time required to generate the prediction is longer than the prediction period. For example, if it takes one hour of computing time in order to predict what will happen to the temperature in the next 10 minutes, why don't I just wait for 10 minutes and measure it for myself? Weather prediction involves complex fluid dynamics modelling of six or more variables with coordinates in a three-dimensional space. The formulas and data are complex and large enough that only a TFLOPS system can effectively produce an accurate answer in a timely manner.
It is true that FLOPS is a more accurate measurement of performance since it counts the number of floating-point operations. However, caution has to be taken with the measurement since not all floating-point processors perform the same set of functions -- some processors, such as x86, include supports for complex mathematical operations (e.g. square-root) while other implementations do not. It is important that we normalize the floating-point operation count so that we can effectively compare the performance of the processors.
Example
In addition to these metrics, we also distinguish the difference between theoretical and actual performance obtainable from a computer system.
Theoretical peak performance
This is the absolute performance limit of a given computer system or device. For example, a computer system equipped with a 500 MHz floating-point co-processor that is capable of delivering a floating-point result per clock cycle is said to have a theoretical peak performance of 500 MFLOPS. Likewise, a computer system equipped with two 500 MHz floating-point co-processors will have a theoretical peak performance of 1 GFLOPS.
Effective, or delivered performance
This is the actual performance obtained from the computer system. Delivered performance must be less than -- and seldom equal to -- the theoretical peak performance. There are many factors that affect the delivered performance of a computer system including the instruction mix and the memory latency. For example, a program consisting of 40% floating-point operations will have a maximum of 200 MFLOPS if the program is run on the computer system described above (500 MFLOPS × 40%). If the entire program is slower by a factor of two because of the memory latency, the delivered performance of the computer system will be 100 MFLOPS (500 MFLOPS × 40%/2).
For example, let's consider three n × n row-major matrices A(i, j), B(i, j), and where (**image**). The general form of any matrix A is defined as follows:
(**image**)
A n × n matrix multiplication operation multiplies the values in matrix A(i, j) with values in matrix B(i, j), and the resulting matrix C(i, j) is governed by the following calculations:
(**image**)
Question 1: how many floating-point add operations are in a matrix multiplication operation?
Answer: There are n - 1 floating point add operations in each  operation, which
are used for calculating the value of each C(i,j) . Since there are n x n entries in C(i,j), therefore the total number of
floating-point operations is n2(n-1)
operation, which
are used for calculating the value of each C(i,j) . Since there are n x n entries in C(i,j), therefore the total number of
floating-point operations is n2(n-1)
Question 2: how many floating-point multiply operations are in a n x n matrix multiplication operation?
Answer: there are n floating-point multiply operations in each  operation, which are used for calculating the value of each
C(i,j). Since there are n x n entries in C(i,j), therefore the toal number of floating-point operations is n3.
operation, which are used for calculating the value of each
C(i,j). Since there are n x n entries in C(i,j), therefore the toal number of floating-point operations is n3.
Question 3: State the floating-point operation performace in terms of n and t, where t is the execution time (in minutes) of the n x n matrix multiplication operation.
Answer: since the total number of floating-point operations in a matrix multiplication operation is equal to the sum of the number of floating-point add and floating-point multiply operations,
therefore the total number of floating-point operations is n3+n2(n-1). Therefore the floating-point performance is 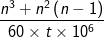 MFLOPS.
MFLOPS.
Question 4: if machine A has a theoretical peak floating-point performance of 800 MFLOPS, how long will it take, in theory, to execute a 1024 x 1024 matrix multiplication operation?
Answer: by substituting performance = 800 MFLOPS and n = 1024 into the equation developed in Question 3, we have:
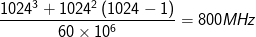
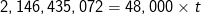
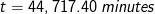
Question 5: how long will it take to execute the same matrix multiplication operation if machine A has an average of 85% delivered performance?
Answer: if machine A has an average of 85% delivered performance, the performance delivered by the machine is 800 MHz×85%. By substituting the values into the equation developed in Question 3, we have:
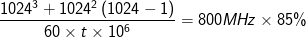
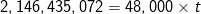
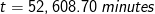
- 9150 reads






