Self-test 2

Available under Creative Commons-ShareAlike 4.0 International License.

An example of a bull market

Assume the probability of an upswing in each period is $\frac{3}{4}$ and that market movements in different periods are independent. Then, the following observation is made over the two-period model:
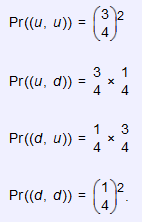Find the probability that there is at least one upswing.

Solution
The event that contains at least one upswing is A = {(u, d), (d, u), (u, u)}. The only event that has all downswings is {(d, d)}; hence:

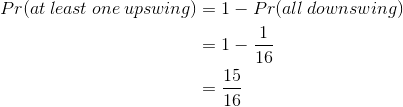
$\begin{align*} Pr(at\: least\: one\: upswing) &=1-Pr(all\:downswing)\\ &=1-\frac{1}{16}\\ &=\frac{15}{16} \end{align*}$

This example illustrates the situation of a bull market, i.e. the probability of an upswing in each period is greater than $\frac{1}{2}$

Now assume that the probability of an upswing in each period is $\frac{1}{4}$ , and that market movements in different periods are independent. This is known as a bear market.

Find the probability that there is at least one downswing over periods of time.

1182 reads

You are here

Self-test 2