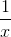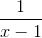Relations and functions

Available under Creative Commons-ShareAlike 4.0 International License.

A relation imposes restrictions on the values of its variables. For instance, when the values of all except one variable of a relation are specified, the possible value(s) of the remaining variable are defined. Note that there can be more than one possible value.

Example 1

1.	For	y = 2x - 3,
		y = -1 when x = 1, y = 1 when x = 2, ...
	that is, there is one possible y for a given x.
2.	For	r² + s² + t² = 1,
		t² = 1 or t = ±1 when r = s = 0, ...
	that is, there are two possible t's for a given pair of r and s.
3.	For	p - 2 > q + 4,
		p > 5 when q = - 1, ...
	that is, there are infinitely many possible p's for a given q.

In general, a relation can involve two or more variables. This module, however, only considers relations of two variables. This section focuses on a special case of relations - functions. To begin, let's review some basic definitions of functions.

Reading

You should now work through the following interactive introduction to the domain and range of a function.

http://www.intmath.com/Functions-and-graphs/2a_Domain-and-range.php.

Example 2

For each of the following equations, discuss whether y is a function of x.

1.	y = x².
2.	y² = x

Solution

1.	y is a function of x since for any given x, y is uniquely defined.
2.	y is not a function of x since for any positive x, y assumes two possible values.

Remark

1.	By convention, the notation f(x) refers to a function of x. Writing f(x) for y assumes that y is a function, so we can write
		f(x) = x² for y = x²
	but not
		f(x)]² = x for y² = x
2.	Although f is commonly used as the name of a function and x and y as variables, you can use other names for identification, including symbols. For example:
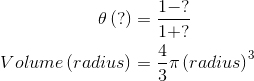
	$\begin{align} \theta \left ( ? \right )&=\frac{1-?}{1+?}\\ Volume\left ( radius \right )&=\frac{4}{3}\pi \left ( radius \right )^{3}\\ \end{align}$
3.	Don't use the same name for different objects (functions or variables) or different names for the same object in the same problem, as this can cause confusion.

You have learned what a function is and how it is defined algebraically. In general, for
	f(x) = an expression of x,
the value of the function f at the point anything is just
	f(anything) = the expression with x replaced by anything.

Example 3

Consider
	F(x) = 2x - 3
The function F at the point anything is
	F(anything) = 2(anything) - 3
1.	If anything = 1, then F(1) = 2(1) - 3.
2.	If anything = t, then F(t) = 2(t) - 3.
3.	If anything = x², then F(x²) = 2(x²) - 3.
4.	If anything = 2x - 3, then F(2x - 3) = 2(2x - 3) - 3

The next example describes how the domain and range of a function are defined.

Example 4

1.	[-2,3] represents the closed interval -2 £ x £ 3.
2.	(1,∞) represents the infinite interval x > 1.
3.	(-16,-9) represents the open interval -16 < x < -9.
4.	[-7,45) represents the half-open interval -7 £ x < 45.
Note that some books use ]a,b[ to denote an open interval.

Note that some books use ]a,b[ to denote an open interval.

T&F uses the symbols '∪' and '∩' to combine two intervals. If you are not familiar with the symbols, just consider that '∪' gives the collection of values in at least one of the two intervals, and '∩' gives the collection of values in both intervals.

Example 5

1.	(-∞,1) ∪ [2,∞) is equivalent to x < 1 or x ³ 2.
2.	(-∞,2) ∩ [1,3) is equivalent to 1 £ x < 2.

Once the domain is defined, the range is implied by the function. Finding the range can be difficult and is sometimes omitted. For the natural domain of a function involving more than one term, we discount the impossible values of individual terms from all real numbers, rather than combine their possible values. To illustrate this point, let's consider the following example.

Example 6

Find the natural domain of the function

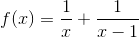
$f(x)=\frac{1}{x}+\frac{1}{x-1}$

Solution

Denominators cannot be zero, so we have the following for individual terms:

Term	Impossible values	Possible values
$\frac{1}{x}$	0	(-∞,0) ∪ (0,∞)
$\frac{1}{x-1}$	1	(-∞,1) ∪ (1,∞)

By removing the impossible values of individual terms, the natural domain consists of all real numbers except 0 and 1, that is,

(-∞,0) ∪ (0,1) ∪ (1,∞)

If we combine the possible values of the two terms, we get all real numbers and that is incorrect.

What you've learned so far in this module has concentrated on algebraic representations of relations. Algebraic representations are important for analysis. However, for the purpose of general understanding or communication, graphical representations can be more efficient.

There are two basic approaches to graph a relation: plotting and sketching. Plotting does not require any pre-knowledge of the graph, you just plot the relation point-by-point over the region of concern. Sketching, on the other hand, uses only a few points, which you then join together using your understanding of the graph. Generally, plotting can be very accurate, but sketching reveals only the general behaviour of a graph and is less time-consuming.

We did not explain how the basic points should be chosen and joined together. Unless we have some idea about what the graph is like, it may not be easy to answer these questions.

Once you understand the basic techniques, graphing is just a mechanical and time-consuming task. This is a typical situation in which algebraic software can really help us save time. The following video activity briefly introduces you to plotting functions using a specialized mathematics software application called Scientific Notebook.

1278 reads

You are here

Relations and functions