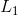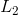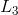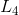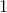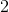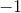Linear functions

Available under Creative Commons-ShareAlike 4.0 International License.

Linear functions are any functions that can be expressed in the form of

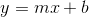
where m and b are constants.

Example 7

1.	2x - 3y = 1 is a linear function.
2.	y = 2 is a special linear function called a constant function.
3.	x = -1 is linear but not a function.
4.	y = x² - 3 is a function but not linear.

To sketch the graph of a linear function, you just need to locate any two points on the graph and then draw a straight line passing through them. This, of course, requires an understanding that the graph of a linear function is a straight line.

A line is defined when we have sufficient information to derive its equation. The next reading discusses various ways to define a line. Note that in the discussion (x,y) represents a general point, and (x1,y1) represents a specific point on the line.

Reading

Read the following sections from an introduction to linear functions from MIT.

http://dedekind.mit.edu/~djk/calculus_beginners/chapter03/section02.html

http://dedekind.mit.edu/~djk/calculus_beginners/chapter03/section03.html

Be sure to try out the applets built into these pages that allow you to experiment with graphing linear functions.

Note that the slope of a vertical line is undefined - not infinity. Slope is an important measure, but is not sufficient to define a line by itself. There are lines of which the slopes are the same.

Example 8

Given that:

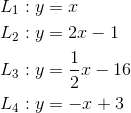
$\begin{align*} L_{1}& : y = x\\ L_{2}& : y = 2x - 1\\ L_{3}& : y =\frac{1}{2}x - 16\\ L_{4}&: y = -x + 3\\ \end{align*}$

Determine which of these lines are:

1.	parallel; or
2.	perpendicular.

Solution

Comparing the above equations with the point-slope equation we obtain

Line	$L_{1}$	$L_{2}$	$L_{3}$	$L_{4}$
Slope			$\frac{1}{2}$

1.	Since the slopes are all different, none of the lines are parallel.
2.	Since the product of Slope(L1) and Slope(L4) is -1, L1 and L4are perpendicular.
(Note that Slope(L₂) × Slope(L₃) = 1, not -1, and therefore L₂ and L₃ are not perpendicular.)

Definition

The equation

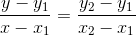
$\frac{y - y_{1}}{x - x_{1}}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

is the two-point equation of the line that passes through the points (x₁,y₁) and (x₂,y₂).

Example 9

Find the equation of the line with x-intercept 2 and y-intercept -1. (Recall that the x-intercept is the x-coordinate where the graph and the x-axis intersect. The y-intercept is the y-coordinate where the graph and the y-axis intersect.)

Solution

The two intercepts imply that (2,0) and (0,-1) are two points on the line. Applying the two-point equation we have

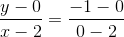
$\frac{y - 0}{x-2}=\frac{-1-0}{0-2}$

Simplifying the equation gives

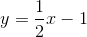
$y=\frac{1}{2}x-1$

1627 reads

You are here

Linear functions