Risk and expected return

Available under Creative Commons-ShareAlike 4.0 International License.

MPT assumes that investors are risk averse, meaning that given two portfolios that offer the same expected return, investors will prefer the less risky one. Thus, an investor will take on increased risk only if compensated by higher expected returns. Conversely, an investor who wants higher expected returns must accept more risk. The exact trade-off will be the same for all investors, but different investors will evaluate the trade-off differently based on individual risk aversion characteristics. The implication is that a rational investor will not invest in a portfolio if a second portfolio exists with a more favorable risk-expected return profile – i.e., if for that level of risk an alternative portfolio exists which has better expected returns.

Note that the theory uses standard deviation of return as a proxy for risk, which is valid if asset returns are jointly normally distributed or otherwise elliptically distributed. There are problems with this, however; see criticism.

Under the model:

Portfolio return is the proportion-weighted combination of the constituent assets' returns.
Portfolio volatility is a function of the correlations ρ_ij of the component assets, for all asset pairs (i, j).

In general:

Expected return:

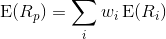
$\operatorname{E}(R_p) = \sum_i w_i \operatorname{E}(R_i) \quad$

where 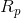R_p is the return on the portfolio, 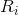R_i is the return on asset i and 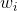w_i is the weighting of component asset 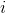(that is, the share of asset i in the portfolio).

Portfolio return variance:

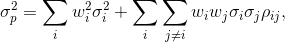
$\sigma_p^2 = \sum_i w_i^2 \sigma_{i}^2 + \sum_i \sum_{j \neq i} w_i w_j \sigma_i \sigma_j \rho_{ij},$

where 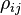$\rho_{ij}$ is the correlation coefficient between the returns on assets i and j. Alternatively the expression can be written as:

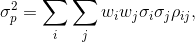
$\sigma_p^2 = \sum_i \sum_j w_i w_j \sigma_i \sigma_j \rho_{ij} ,$

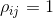where $\rho_{ij} = 1$ for i=j.

Portfolio return volatility (standard deviation):

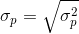
$\sigma_p = \sqrt {\sigma_p^2}$

For a two asset portfolio:

Portfolio return: 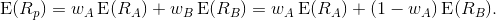$\operatorname{E}(R_p) = w_A \operatorname{E}(R_A) + w_B \operatorname{E}(R_B) = w_A \operatorname{E}(R_A) + (1 - w_A) \operatorname{E}(R_B).$

Portfolio variance: 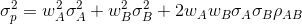$\sigma_p^2 = w_A^2 \sigma_A^2 + w_B^2 \sigma_B^2 + 2w_Aw_B \sigma_{A} \sigma_{B} \rho_{AB}$

For a three asset portfolio:

Portfolio return: 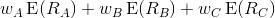$w_A \operatorname{E}(R_A) + w_B \operatorname{E}(R_B) + w_C \operatorname{E}(R_C)$

Portfolio variance: 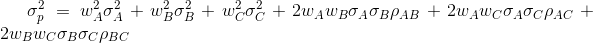$\sigma_p^2 = w_A^2 \sigma_A^2 + w_B^2 \sigma_B^2 + w_C^2 \sigma_C^2 + 2w_Aw_B \sigma_{A} \sigma_{B} \rho_{AB} + 2w_Aw_C \sigma_{A} \sigma_{C} \rho_{AC} + 2w_Bw_C \sigma_{B} \sigma_{C} \rho_{BC}$

瀏覽次數：1338

您在這裡

Risk and expected return