The CAPM is a model for pricing an individual security or portfolio. For individual securities, we make use of the security market line (SML) and its relation to expected return and systematic risk (beta) to show how the market must price individual securities in relation to their security risk class. The SML enables us to calculate the reward-to-risk ratio for any security in relation to that of the overall market. Therefore, when the expected rate of return for any security is deflated by its beta coefficient, the reward-to-risk ratio for any individual security in the market is equal to the market reward-to-risk ratio, thus:
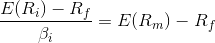
The market reward-to-risk ratio is effectively the market risk premium and by rearranging the above equation and solving for E(Ri), we obtain the Capital Asset Pricing Model (CAPM).
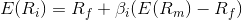
where:
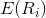is the expected return on the capital asset
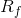is the risk-free rate of interest such as interest arising from government bonds
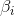(the beta) is the sensitivity of the expected excess asset returns to the
expected excess market returns, or also 
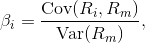
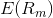is the expected return of the market
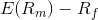is sometimes known as the market premium (the difference between
the expected market rate of return and the risk-free rate of return).
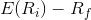is also known as the risk premium
Restated, in terms of risk premium, we find that:
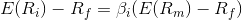
which states that the individual risk premium equals the market premium times β.
Note 1: the expected market rate of return is usually estimated by measuring the Geometric Average of the historical returns on a market portfolio (e.g. S&P 500).
Note 2: the risk free rate of return used for determining the risk premium is usually the arithmetic average of historical risk free rates of return and not the current risk free rate of return.
For the full derivation see Modern portfolio theory.
- 瀏覽次數：1351
