Some statements in the above proof were simple, e.g., the single proposition "A − has − 2". Some statements had several parts, though, e.g., "(F − unsafe and G − unsafe)". We build these more complicated statements out of propositions. If you know both F − unsafe is false, and G − unsafe is false, what can you deduce about the truth of the statement "(F − unsafe and G − unsafe)"? Clearly, it is also false. What about when F − unsafe is false, but G − unsafe is true? What about when both propositions are true? In fact, we can fill in the following table:
|
A |
B |
(a^b) |
|
false |
false |
False |
|
false |
true |
False |
|
true |
false |
false |
|
true |
true |
true |
Definition 2.3: truth table
A truth table for an expression has a column for each of its propositional variables. It has a row for each different true/false combination of its propositional variables. It has one more column for the expression itself, showing the truth of the entire expression for that row.
Exercise 2.1.1.1
What do you think the truth table for "a or b" looks like? Hint: To fill out one row of the table, say, for a = true and b = false, ask yourself "For this row, is it true that (a is true, or b is true)?"
Exercise 2.1.1.2
The above proof also used subexpressions of the form "not b-unsafe". What is the truth table for "not a"?
Exercise 2.1.1.3
What is the truth table for the expression "(not a) or b"?
Definition 2.4: connective
- The syntactic operator combining one or more logical expressions into a larger expression.
Example
Two operators are ∧ and ∨.
- A function with one or more Boolean inputs and a Boolean result. I.e., the meaning of a syntactic operator.
Example
The meaning of ∧ and ∨, e.g., as described by their truth tables.
Example
nand (mnemonic: "not and"), written ↑, takes in two Boolean values a and b, and returns true exactly when a ∧ b is not true that is, a ↑ b ≡¬ (a ∧ b).
The following are the connectives we will use most often. At least some of these should already be familiar from Boolean conditional expressions.
|
Connective |
Pronunciation |
Meaning |
Alternative pronunciations / notations |
|
|
not |
|
-a; !a |
|
|
and |
|
a*b; ab; a&&b; a&b |
|
|
or |
|
a+b; a||b; a|b |
|
|
implies |
|
|
Many other connectives can also be defined. In fact, it turns out that any connective for propositional logic can be defined in terms of those above.
Example 2.1
Another connective is if-and-only-if or iff, written as a ⇔ b, which is true when a and b have the same truth value. So, as its name implies, it can be defined as (a ⇒ b) ∧ (b ⇒ a). It is also commonly known as "a is equivalent to b" and "a is necessary and sufficient for b".
Exercise 2.1.1.4
Another connective is "exactly-one-of", which is more traditionally called exclusive-or or xor (since it excludes both a and b holding, unlike the traditional "inclusive" or.) How would you define a "xor" b in terms of the above connectives?
Note that the conventional a ∨ b is sometimes called inclusive-or, to stress that it includes the case where both a and b hold. In English, the word "or" may sometimes mean inclusive-or, and other times mean exclusive-or, depending on context. Sometimes the term "andjor" is used to emphasize that the inclusive-or really is intended.
Exercise 2.1.1.5
For each of the following English sentences, does "or" mean inclusive-or or exclusive-or?
- "Whether you are tired or lazy, caffeine is just the drug for you!"
- "Whether you win a dollar or lose a dollar, the difference in your net worth will be noticed."
- "If you own a house or a car, then you have to pay property tax."
- "Give me your lunch money, or you'll never see your precious hoppy taw again"
- 5786 reads





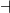
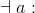 a is false
a is false
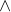
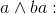 and b are both true
and b are both true
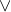
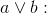 at least one of {a,b} is true
at least one of {a,b} is true
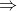
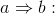 equivalent to
equivalent to 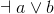
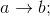
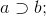 if a then b; a only if b; b if a; b is necessary for
a; a is sufficient for b
if a then b; a only if b; b if a; b is necessary for
a; a is sufficient for b

