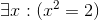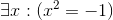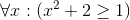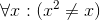Available under Creative Commons-ShareAlike 4.0 International License. Download for free at http://cnx.org/contents/383d4b87-2d7b-454e-99fe-2eaa43eae8ff@20.20
Exercise 4.4.8
Let P (x) be the statement "has been to Prague", where the domain consists of your classmates.
- Express each of these quantifcations in English.
- ∃x :(P (x))
- ∀x :(P (x))
- ¬∃x :(P (x))
- ¬∀x :(P (x))
- ∃x :(¬P (x))
- ∀x :(¬P (x))
- ¬∃x :(¬P (x))
- ¬∀x :(¬P (x))
- Which of these mean the same thing?
Exercise 4.4.9
Let C (x) be the statement "x has a cat", let D (x) be the statement "x has a dog", and let F (x) be the statement "x has a ferret". Express each of these statements in first-order logic using these relations. Let the domain be your classmates.
- A classmate has a cat, a dog, and a ferret.
- All your classmates have a cat, a dog, or a ferret.
- At least one of your classmates has a cat and a ferret, but not a dog.
- None of your classmates has a cat, a dog, and a ferret.
- For each of the three animals, there is a classmate of yours that has one.
Exercise 4.4.10
Determine the truth value of each of these statements if the domain is all real numbers. Where appropriate, give a witness.
- 4146 reads