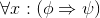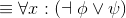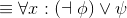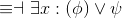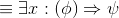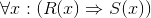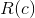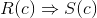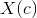Solutions to Exercises in Chapter .

Solution to Exercise 4.1.1.1

The cue "Somebody ..." suggests one person who exists; we'll call them p for "popular": ∃p :(... ). Now we need to fill in the dots with "everybody likes p", to get: ∃p :(∀x : (likes (x, p))).

Solution to Exercise 4.1.1.2

The cue "Everybody ..." suggests a universal; we'll call them j for "J. Doe": ∀j :(... ). Now we need to fill in the dots with "somebody likes j", to get: ∀j :(∃x : (likes (x, j))). Note that this formula is just like the preceding "Somebody likes everybody" example (Example 4.3), except that the quantifiers have been swapped (and different variable names were used, a superficial difference).

Solution to Exercise 4.1.1.3

"Evenness" is a straightforward translation from " An integer n is even, if it is twice some other integer k ": even (n) ≡∃k :(n =2k). Note that by this standard definition, zero is even.

There are many equivalent ways to define primality, just as there many algorithms for checking primality. One straightforward solution is noncomposite (n) ≡∀j :(∀k : ((jk = n) ⇒ (j = 1) ∨ (k = 1))). Well, this is almost expresses "prime", except that n =1 satisfes this formula. A mathematician points out that just as 0 is neither positive nor negative, 1 is neither prime nor composite; as stated this formula actually captures "noncomposite", oops. There are several ways to upgrade this to exactly capture "prime".

ASIDE: 1 is called a "unit". If we consider the domain of all integers (not just natural numbers), the idea of primality still makes sense; -17 is also prime; and -1 is also another unit. Similarly, considering the domain of "complex integers" {a, b, a + bi | a ∈ Z ∧ b ∈ Z} (could be written " Z+ Zi "), then i and −i are also units. How might we generalize our defnition of prime, to work in these further interpretations?

A similar, equivalent formula to the above is noncomposite(n)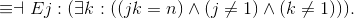

Solution to Exercise 4.1.1.4

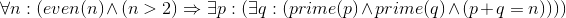
Solution to Exercise 4.1.1.5

We need a new relation that combines the syntax of < and size. The result would look like less − than − size (i, a). This assumes the new relation has the obvious intended defnition.

Solution to Exercise 4.1.1.6

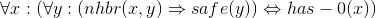
Solution to Exercise 4.1.1.7

There are various solutions, but they all must capture the same idea: there exists exactly one unsafe neighbor. This solution states that in two parts:

Together, these two parts imply there is only one such u.

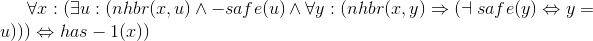
Solution to Exercise 4.2.1.1

Solution to Exercise 4.3.1.1

In line 4, ∀Intro requires that variable being generalized, q, be arbitrary. It was introduced in line 2 by ∀Elim, so that's OK. (E.g., we could've used ∀Intro on line 3 to reintroduce the quantifer just eliminated.) But, q was free when we used ∃Elim on line 3, and this makes the variable no longer arbitrary. Line 3's choice of p may depend on q, and a variable is only arbitrary if it is free of any such constraints.

Solution to Exercise 4.4.5

ASIDE: More interestingly though, imagine we did interpret piratesNextTo over the domain N only. We could then pretend that the locations, instead of being named A,...,Z, were just numbered 1,...,24. While this representation doesn't refect how we model the problem, it is legal. Exercise for the reader: Write a formula which excludes relation piratesNextTo which can't match this convention!

Solution to Exercise 4.4.16

One interpretation that satisfes this is a domain of three people Alice, Bob, Charlie, with the likes relation: {(Alice, Bob) , (Bob, Bob)}. Bob is liked by two people, so it satisfies the statement.

Here's another interpretation that is the same except for renaming, and thus not fundamentally different: a domain of three people Alyssa, Bobby, Chuck, with the likes relation: {(Chuck, Alyssa) , (Alyssa, Alyssa)}. With the substitutions [Chuck→Alice] and [Alyssa→Bob], we see that the underlying structure is the same as before.

Here's an interpretation that is fundamentally different: a domain of three people Alice, Bob, Charlie, with the likes relation: {(Charlie, Bob) , (Alice, Bob)}. No matter how you rename, you don't get somebody liking themself, so you can see its underlying structure is truly different than the preceding interpretations.

English is fuzzy enough that it is unclear whether "one" and "two" are meant as exact counts. The above two examples each assumed they are.

ASIDE: If we change the statement slightly to add a comma: " There exists one person, who is liked by two people ", we arguably change the meaning signifcantly. The now-independent first clause arguably means there is only one person existent in total, so the overall statement must be falsel There's a quick lesson in the diference between English dependent and independent clauses.

Solution to Exercise 4.4.28