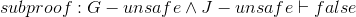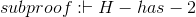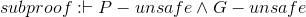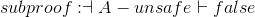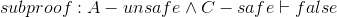Now let's use these rules in a couple larger proofs, to show some more interesting results.
Example 2.20
Let's redo the first example (Example 2.11)'s proof formally and show 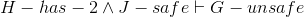
The inference rules we used informally above don't correspond exactly to those in our defnition, so the formal proof is more complicated.
| 1 |
H − has − 2 ⇒ P − unsafe ∧ G − unsafe ∨ J − unsafe ∧ P − unsafe ∨ G − unsafe ∧ J − unsafe |
WaterWorld axiom, choosing a grouping of the ternary ∨, as justifed by ∨ commutativity (Example 2.14) |
|
|
2 |
H − has − 2 ∧ J − safe |
Premise |
|
|
3 |
H − has − 2 |
∧Elim (left), line 2 |
|
|
4 |
P − unsafe ∧ G − unsafe ∨ J − unsafe ∧ P − unsafe ∨ G − unsafe ∧ J − unsafe |
⇒Elim, lines 1,3 |
|
|
5 |
J − safe |
∧Elim (right), line 2 |
|
|
6 |
J − safe ⇒ ¬J − unsafe |
WaterWorld axiom |
|
|
7 |
¬J − unsafe |
⇒Elim, lines 5,6 |
|
|
8 |
|
||
|
8.a |
G − unsafe ∧ J − unsafe |
Premise for subproof |
|
|
8.b |
J − unsafe |
∧Elim (right), line 8.a |
|
| 8.c |
false |
falseIntro, lines 7,8.b |
|
|
9 |
¬ (G − unsafe ∧ J − unsafe) |
RAA, line 8 |
|
|
10 |
P − unsafe ∧ G − unsafe ∨ J − unsafe ∧ P − unsafe |
CaseElim (right), lines 4,9 |
|
|
11 |
subproof:J − unsafe ∧ P − unsafe f false |
||
|
11.a |
J − unsafe ∧ P − unsafe |
Premise for subproof |
|
|
11.b |
J − unsafe |
∧Elim (left), line 11.a |
|
|
11.c |
false |
falseIntro, lines 7,11.b |
|
|
12 |
¬ (J − unsafe ∧ P − unsafe) |
RAA, line 11 |
|
|
13 |
P − unsafe ∧ G − unsafe |
CaseElim (right), lines 10,12 |
|
|
14 |
G − unsafe |
∧Elim (right), line 13 |
|
Wow! This formalization is a lot longer than the original informal proof. That's a result of the particular set of inference rules we are using, that we can only make inferences in small steps. Also, here we were pickier about the distinction between "not safe" and "unsafe".
Example 2.21
The previous example (Example 2.20) is a perfect candidate for adding structure to the proof by using additional subproofs. The following is more similar to the original informal proof
(Example 2.11).
Note also that subproofs can have their own subproofs.
| 1 | H − has − 2 ⇒ P − unsafe ∧ G − unsafe ∨ J − unsafe ∧ P − unsafe ∨ G − unsafe ∧ J − unsafe | WaterWorld axiom, choosing a grouping of the ternary ∨, as justied by ∨ commutativity (Example 2.14) | ||
| 2 |
|
|||
| 2.a | H − has − 2 ∧ J − safe |
Premise |
||
| 2.b | H − has − 2 | ∧Elim (left), line 2.a | ||
| 3 | P − unsafe ∧ G − unsafe ∨ J − unsafe ∧ P − unsafe ∨ G − unsafe ∧ J − unsafe | ⇒Elim, lines 1,3 | ||
| 4 |
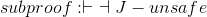
|
|||
| 4.a | H − has − 2 ∧ J − safe | Premise | ||
| 4.b | J − safe | ∧Elim (right), line 4.a | ||
| 4.c | J − safe ⇒ ¬J − unsafe | WaterWorld axiom | ||
| 4.d | ¬J − unsafe | ⇒Elim, lines 4.b,4.c | ||
| 5 |
|
|||
| 5.a |
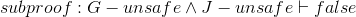
|
|||
| 5.a.i | G − unsafe ∧ J − unsafe |
Premise for subproof |
||
| 5.a.ii | J − unsafe | ∧Elim (right), line 5.a.1 | ||
| 5.a.iii | false | falseIntro, lines 4,5.a.2 | ||
| 5.b | ¬ (G − unsafe ∧ J − unsafe) | RAA, line 5.a | ||
| 5.c | P − unsafe ∧ G − unsafe ∨ J − unsafe ∧ P − unsafe | CaseElim (right), lines 3,5.b | ||
| 5.d |
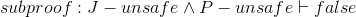
|
|||
| 5.d.i | J − unsafe ∧ P − unsafe | Premise for subproof | ||
| 5.d.ii | J − unsafe | ∧Elim (left), line 5.a.1 | ||
| 5.d.iii | false | falseIntro, lines 4,5.d.2 | ||
| 5.e | ¬ (J − unsafe ∧ P − unsafe) | RAA, line 5.d | ||
| 5.f | P − unsafe ∧ G − unsafe | CaseElim (right), lines 5.c,5.e | ||
| 6 | G − unsafe | ∧Elim (right), line 5 | ||
A standard way of presenting proofs is by using lemmas to show parts of the proofs. Lemmas are simply formulas which we prove not as an end result, but as intermediate steps in a larger proof. So, they are simply another way of presenting subproofs.
Example 2.22
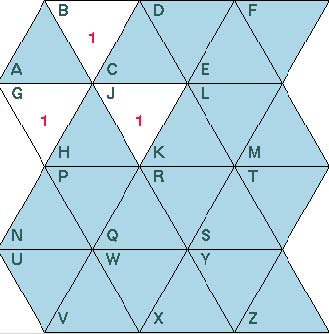
Consider the above figure (Figure 2.6). We'll show B − has − 1 ∧ G − has − 1 ∧ J − has − 1 f K − unsafe. We'll do this through the following series of lemmas:
- Lemma A:
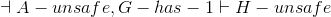
- Lemma B:
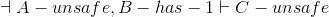
- Lemma C:
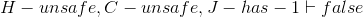
- Lemma D:
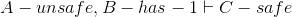
- Lemma E:
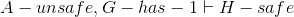
- Lemma F:
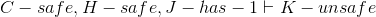
First, we'll show the main proof, assuming each of the lemmas. Then, proofs of each of the lemmas will follow.
| 1 |
B − has − 1 ∧ G − has − 1 ∧ J − has − 1 |
Premise | |
| 2 |
B − has − 1 |
∧Elim (left), line 1 | |
| 3 |
G − has − 1 ∧ J −has − 1 |
∧Elim (right), line 1 | |
| 4 |
G − has − 1 |
∧Elim (left), line 3 | |
| 5 |
J − has − 1 |
∧Elim (right), line 3 | |
| 6 |
|
||
| 6.a |
¬A − unsafe |
Premise for subproof | |
| 6.b |
H − unsafe |
Lemma A, lines 6.a,4 | |
| 6.c |
C − unsafe |
Lemma B, lines 6.a,2 | |
| 6.d | false | Lemma C, lines 6.b,6.c,5 | |
| 7 |
A − unsafe |
RAA, line 6 | |
| 8 |
C − safe |
Lemma D, lines 7,2 | |
| 9 |
H − safe |
Lemma E, lines 7,3 | |
| 10 |
K − unsafe |
Lemma F, lines 8,9,5 | |
And that's the desired proof! Now it just remains to show each of the six lemmas.
Lemma A: 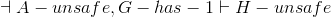
| 1 | ¬A − unsafe |
Premise |
|
| 2 | G − has − 1 |
Premise |
|
| 3 |
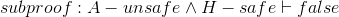
|
||
| 3.a | A − unsafe ∧ H − safe | Premise for subproof | |
| 3.b | A − unsafe | ∧Elim | |
| 3.c | false | falseIntro, lines 1,3b | |
| 4 | ¬ (A − unsafe ∧ H − safe) | RAA, line 3 | |
| 5 | G − has − 1 ⇒ A − safe ∧ H − unsafe ∨ A − unsafe ∧ H − safe | WaterWorld axiom | |
| 6 | A − safe ∧ H − unsafe ∨ A − unsafe ∧ H − safe | ⇒Elim, lines 5,2 | |
| 7 | A − unsafe ∧ H − safe ∨ A − safe ∧ H − unsafe | Theorem: ∨ commutes, line 6 | |
| 8 | A − safe ∧ H − unsafe | CaseElim, lines 4,7 | |
| 9 | H − unsafe | ∧Elim (right), line 8 | |
Lemma B: 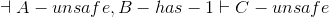
| 1 | ¬A − unsafe | Premise | |
| 2 | B − has − 1 | Premise | |
| 3 |
|
||
| 3.a | A − unsafe ∧ C − safe | Premise for subproof | |
| 3.b | A − unsafe | ∧Elim (left), line 3a | |
| 3.c | false | falseIntro, lines 1,3b | |
| 4 | ¬ (A − unsafe ∧ C − safe) | RAA, line 3 | |
| 5 | B − has − 1 ⇒ A − safe ∧ C − unsafe ∨ A − unsafe ∧ C − safe | WaterWorld axiom | |
| 6 |
A − safe ∧ C − unsafe ∨ A − unsafe ∧ C − safe |
⇒Elim, lines 5,2 | |
| 7 | A − unsafe ∧ C − safe ∨ A − safe ∧ C − unsafe | Theorem: ∨ commutes, line 6 | |
| 8 | A − safe ∧ C − unsafe | CaseElim, lines 4,7 | |
| 9 | C − unsafe | ∧Elim (right), line 8 | |
Proving the other lemmas is left as an exercise to the reader.
Note that we took a little shortcut: we used the lemmas as if they were inference rules. According to our previous definition of proofs, we technically should present the lemma as a subproof
and then use an inference rule or two to show how that applies, as we've done in previous examples. This shorter form is common practice and much easier to read.
In summary, we must state one of the following four possible reasons for each step in a proof, allowing subproofs.
- This step's WFF is a premise.
- This step's WFF is an axiom.
- This step's WFF follows from a inference rule applied to previous steps' WFFs. The reason includes a statement of which inference rule is used and how.
- This step's WFF follows from a subproof, where that subproof may temporarily introduces additional premises. The reason includes the entire subproof. When that subproof has been shown elsewhere, such as in class or another exercise, it may simply be cited, for brevity. Of course, subproofs may have additional embedded subproofs, in turn.
Technically, when using subproofs, one must be careful to rename variables, to avoid clashes. Rather than formalize this notion, we'll leave it as "obvious".
- 3674 reads