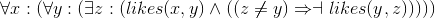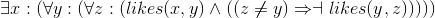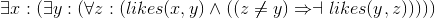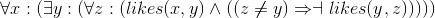Exercise 4.4.11
Let P (x), Q (x), R (x), and S (x) be the statements "x is a duck", "x is one of my poultry", "x is an officer", and "x is willing to waltz", respectively. Express each of these statements using quantifiers, logical connectives, and the relations P (x), Q (x), R (x), and S (x).
- No ducks are willing to waltz.
- No ofcers ever decline to waltz.
- All my poultry are ducks.
- My poultry are not ofcers.
- Does the fourth item follow from the first three taken together? Argue informally; you don't need to use the algebra or inference rules for first-order logic here.
Exercise 4.4.12
You come home one evening to find your roommate exuberant because they have managed to prove that there is an even prime number bigger than two. More precisely, they have a correct proof of ∃y :(P (y) ∧ (y> 2) ⇒ E (y)), for the domain of natural numbers, with P interpreted as "is prime?" and E interpreted as "is even?". While they are celebrating their imminent fame at this amazing mathematical discovery, you ponder...
- ...and realize the formula is indeed true for that interpretation. Briefy explain why. You don't need to give a formal proof using Boolean algebra or inference rules; just give a particular value for y and explain why it satisfes the body of " ∃y :(y) ".
- Is the formula still true when restricted to the domain of natural numbers two or less? Briefy explain why or why not.
- Is the formula still true when restricted to the empty domain? Briefy explain why or why not.
- Give a formula that correctly captures the notion " there is an even prime number bigger than 2 ".
Exercise 4.4.13
For the sentence ∀x :(∀y :(A (x) ∧ B (x, y) ⇒ A (y))) state whether it is true or false, relative to the following interpretations. If false, give values for x and y witnessing that.
- The domain of the natural numbers, where A is interpreted as "even?", and B is interpreted as "equals"
- The domain of the natural numbers, where A is interpreted as "even?", and B is interpreted as "is an integer divisor of"
- The domain of the natural numbers, where A is interpreted as "even?", and B is interpreted as "is an integer multiple of"
- The domain of the Booleans, {true, false}, where A is interpreted as "false?", and B is inter preted as "equals"
- The domain of WaterWorld locations in the particular board where locations Y and Z contain pirates, but all other locations are safe, the relation symbol A is interpreted as "unsafe?", and B is interpreted as "neighbors"
- All WaterWorld boards, where A is interpreted as "safe?” and B is interpreted as "neighbors". (That is, is the formula valid for WaterWorld?)
Exercise 4.4.14
Translate the following conversational English statements into first-order logic, using the suggested predicates, or inventing appropriately-named ones if none provided. (You may also freely use = which we'll choose to always interpret as the standard equality relation.)
- "All books rare and used". This is claimed by a local bookstore; what is the intended domain? Do you believe they mean to claim "all books rare or used"?
- " Everybody who knows that UFOs have kidnapped people knows that Agent Mulder has been kidnapped. " (Is this true, presuming that no UFOs have actually visited Earth...yet?)
Exercise 4.4.15
Write a formula for each of the following. Use the two binary relations isFor and isAgainst and domain of all people.
- "All for one, and one for alll" We'll take "one" to mean "one particular person", and moreover, that both "one"s are referring the same particular person, resulting in "There is one whom everybody is for, and that one person is for everybody." 13
- "If you're not for us, you're against us." In aphorisms, "you" is meant to be an arbitrary person; consider using the word "one" instead. Furthermore, we'll interpret "us" as applying to everybody. That is, " One always believes that 'if one is not for me, then one is against me' ".
- "The enemy of your enemy is your friend." By "your enemy" we mean "somebody you are against", and similarly, "your friend" will mean "somebody you are for". (Be carefulel This may be different than "somebody who is againstjfor you").
- "Somebody has an enemy." (We don't know of an aphorism expressing this. 14 )
- Two interpretations are considered fundamentally the same (or isomorphic) if you can map one interpretation to the other simply by a consistent renaming of domain elements.
Exercise 4.4.16
Find two fundamentally different interpretations that satisfy the statement "There exists one person who is liked by two people".
Exercise 4.4.17
For the four "Musketeer" formulas from a previous exercise (Exercise 4.4.15), find three fundamentally different interpretations of isFor which satisfy all the formulas on a domain of three
people.
Depict each of these interpretations as a graph. Draw three circles (nodes) representing the three people, and an arrow (edge) from
a person to each person they like. (You can glance at Rosen Section 9.1, Figure 8 for an example.)
Exercise 4.4.18
Translate the following statements into first-order logic. The domain is the set of natural numbers, and the binary relationkth
(k, n) indicates whether or not the kth
number of the sequence is n. For example, the sequence (5, 7, 5), is represented by the relation kth = {(0, 5) , (1, 7) , (2, 5)}. You can also use the binary
relations =, <, and ≤, but no others.
You may assume that kth models a sequence. No index k is
occurs multiple times, thus excluding kth = {(0, 5) , (1, 7) , (0,
9)}. Thus, kth is a function, as in a previous example representing an array as a function (Example 4.8). Also,
no higher index k occurs without all lower-numbered indices being present, thus excludingkth
= {(0, 5) , (1, 7) , (3, 9)}.
- The sequence is fnite.
- The sequence contains at least three distinct numbers , e.g., (5, 6, 5, 6, 7, 8), but not (5, 6, 5, 6).
- The sequence is sorted in non-decreasing order, e.g., (3, 5, 5, 6, 8, 10, 10, 12).
- The sequence is sorted in non-decreasing order, except for exactly one out-of-order element, e.g., (20, 30, 4, 50, 60).
Exercise 4.4.19
Some binary relations can be viewed as the encoding of a unary function, where the first element of the ordered pair represents the function's value. For instance, in a previous exercise (Exercise 4.4.2) we encoded the binary function addition as a ternary relation addsTo.
- Give one example of a binary relation which does not correspond to the encoding of a function.
- Write a first-order formula describing the properties that a binary relation R must have to correspond to a unary function.
Exercise 4.4.20
Alternation of quantifiers: Determine the truth of each of the following sentences in each of the indicated domains.
Four sentences:
Four domains:
- The empty domain.
- A world with one person, who likes herself.
- A world with Yorick and Zelda, where Yorick likes Zelda, Zelda likes herself, and that's all.
- A world with many people, including CJ (Catherine Zeta-Jones), JC (John Cusack), and JR (Julia Roberts). Everybody likes themselves; everybody likes JC; everybody likes CJ except JR; everybody likes JR except CJ and IB. Any others may or may not like each other, as you choose, subject to the preceding. (You may wish to sketch a graph of this likes relation, similar to Rosen Section 9.1 Figure 8.)
Determine the truth of all sixteen combinations of the four statements and four domains.
- 4917 reads