Is the formula A − unsafe∨ A − has − 2 true? Your response should be that it depends on the particular board in question. But some formulas are true regardless of the board. For instance, A − unsafe ∨¬A − unsafe: this holds no matter what. Similarly, A − unsafe ∧¬A − unsafe can never be satisfied (made true), no matter how you try to set the variable A − unsafe.
Definition 2.6: truth assignment
An assignment of a value true or false to each proposition being used.
Example
For the formula a ⇒ a ∧ b, one possible truth assignment is a = true and b = false. With that truth assignment, the formula is false.
ASIDE: We've used three different symbols to describe "equality" in some sense:
- a ⇔ b is a formula. The symbol "⇔" is a logical connective.
- φ ≡ ψ is a statement that two formulas are equivalent −−− that is, the same for all truth assignments.
- a = true defines the value of a proposition. We also use the symbol for defining variables, b = ψ, and meta-variables, φ = ψ.
Of these, only "⇔" occurs within a formula.
Commonly, people use symbols such as "≡" for multiple purposes. This is problematic when part of what we are studying are the syntactic formulas themselves.
Definition 2.7: tautology
A WFF which is true under any truth assignment (any way of assigning true/false to the propositions).
Example
A − unsafe ⇒ A − unsafe
Example
a ⇒ a ∨ b
Definition 2.8: unsatisfable
A WFF which is false under any truth assignment.
Example
¬ (A − unsafe ⇒ A − unsafe)
Example
a ⇒¬a
Note that in algebra, there are certainly formulas which are true (or similarly, false) for all values, but they don't get special names. For example, over the real numbers, any assignment to x makes the formula x2 ≥ 0 true, so it's similar to a tautology. Similarly, x = x +1 is unsatisfable, since it can't be made true for any assignment to x.
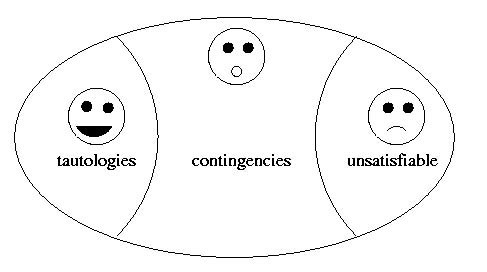
Some people use the term contingency to mean formulas in between: things which can be either true or false, depending on the truth assignment. Really, tautologies and unsatisfable formulas are boring. However, trying to determine whether or not a formula is a tautology (or, unsatisfable) is of interest. That's what proofs are all aboutl
Identify the following Yogi Berra quotes either as tautologies, unsatisfiable, or neither. (Take these exercises with a grain of salt, since the English statements are open to some interpretation.)
Exercise 2.1.2.1
" Pitching always beats batting −−− and vice-versa. "
Exercise 2.1.2.2
You can observe a lot just by watchin'.
Exercise 2.1.2.3
Nobody goes there anymore... it's too crowded.
Exercise 2.1.2.4
It sure gets late early out here.
Exercise 2.1.2.5
Always go to other people's funerals; otherwise they won't come to yours.
- 4699 reads






