What are the roots of x3 − 4x? Well, in high-school algebra you learned how to deal with such numeric formulas:
|
x3 – 4x |
||
|
= |
x(x2-4) |
factor out x |
|
= |
x(x-2)(x+2) |
The identity a2 – b2 = (a + b)(a-b) with a being x, and b being 2. |
This last expression happens to be useful since it is in a form which lets us read of the roots 0, +2, -2. The rules of algebra tell us that these three different formulas are all equivalent. In fact, our very definition of two formulas being equivalent is that for any value of x the two formulas return the same value. We are distinguishing between syntax (the expression itself, as data), and semantics (what the expression means). Usually, when presented with syntax, one is supposed to bypass that and focus on its meaning (e.g., reading a textbook). However, in logic and post-modern literature alike, we are actually studying the interplay between syntax and semantics. The general gist is that in each step, you rewrite subparts of your formula according to certain rules ("replacing equals with equals").
Well, we can use a similar set of rules about rewriting formulas with equivalent ones, to answer the questions of whether two formulas are equal, or whether a formula is a tautology. George Boolell was the first to realize that true and false are just values in the way that numbers are, and he first codified the rules for manipulating them; thus Boolean algebra is named in his honor.
ASIDE: The term "algebral2 " comes from the values true, false and operators ∧, ∨ having some very specific properties similar to those of numbers with ×, +.

Again, each individual step consists of rewriting a formula according to certain rules. So, just what are the rules for manipulating Boolean values? We'll start with an example.
Example 2.4
|
1 |
a ∧ false ∨ b ∧ true |
|
|
2 |
≡false ∨ b ∧ true |
Dominance of false over ∧ |
|
3 |
≡b ∧ true ∨ false |
Commutatively of ∨ |
|
4 |
≡b ∧ true |
Identity element for ∨ is false |
|
5 |
≡b |
Identity element for ∧ is true |
Thus we have a series of equivalent formulas, with each step justified by citing a Propositional equivalences. By and large, the equivalences are rather mundane. A couple are surprisingly handy; take a moment to consider DeMorgan's laws.
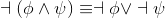
|
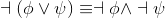
|
(Try φ being "Leprechauns are green", and ψ being "Morgana Le Fay likes gold". Do these laws make sense, for each of the four possible truth assignments?) Augustus DeMorganl was also an important fgure in the formalization of logic.

Here is another example. For a statement φ ⇒ ψ, the contrapositive of that formula is ¬ψ ⇒¬φ. We can show that a formula is equivalent to its contrapositive:
Example 2.5
|
1 |
φ⇒ψ |
|
|
2 |
≡¬φ∨ψ |
Definition of ⇒ |
|
3 |
≡ψ∨¬φ |
Commutativity of ∨ |
|
4 |
≡¬¬ψ∨¬φ |
Double Complementation |
|
5 |
≡¬ψ⇒¬φ |
Definition of ⇒ |
Don't confuse the contrapositive of a statement with the converse of a formula: The converse of φ ⇒ ψ is the formula ψ ⇒ φ; in general a formula is not equivalent to its converse!
This next example is actually a proof of one of the laws from the given list, using (only) others from the list.
Example 2.6
|
1 |
φ∧ψ∧ψ |
|
|
2 |
≡φ∧ψ∧ψ∧ true |
Identity of ∧ |
|
3 |
≡ψ∧φ∧ψ∧ true |
Commutativity of ∨ |
|
4 |
≡ψ∧(φ∨ true) |
Distributivity of ∧ over ∨ |
|
5 |
≡ψ∧ true |
Domicance of ∨ |
|
6 |
≡ψ |
Identity of ∧ |
Exercise 2.3.1.1
Show that the "Absorption of ∧" equivalence holds, given the other equivalences. I.e., show (a ∨ b) ∧ b ≡ b.
Compared to proofs using truth tables, Boolean algebra gives us much shorter proofs. But, determining which equivalence to use in the next step of a proof can be difcult. In this case,
compare the solution for this exercise to the previous absorption proof. These two proofs have a special dual relationship described in the next section.
Exercise 2.3.1.2
Show that the modus ponens rule, a ∧ (a ⇒ b) ⇒ b always holds. I.e., show that it is a tautology, and thus equivalent to
true.
So, what would it mean to use Boolean algebra as reasoning for WaterWorld? That is, if you wanted to show that G − safe was true, how would you do that using Boolean algebra?
As with truth-tables, we would take the conjunction of all the WaterWorld domain axioms (call it ρ), and the board's observed state (ψ). We would then want to show
that asserting G − safe was already equivalent to the rules-and-observed-state: ρ ∧ ψ ≡ ρ ∧ ψ ∧ G − safe.
- 4560 reads






