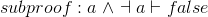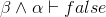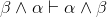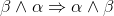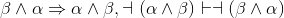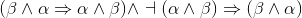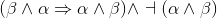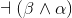Subproofs

This is known as proof-by-contradiction. We start by making a single unproven assumption. We then try to prove that false is true. Clearly, that it nonsense, so we must have done something wrong. Assuming we didn't make any mistakes in the individual inference steps, then the only thing that could be wrong is the assumption. It must not hold. Therefore, we have just proven its negation.

This form of reasoning is often expressed via contrapositive. Consider the slogan

If you paid list price, you didn't buy it at SuperMegaMart.

(This is a contrapositive, because the real statement the advertisers want to make is that if you buy it at SuperMegaMart, then you won't pay list price.), which we'll abbreviate payFull ⇒¬boughtAtSMM. You know this slogan is true, and you just made a SuperMegaMart purchase (boughtAtSMM), and are suddenly wanting a proof that you got a good deal. Well, suppose we didn't. That is, suppose payFull. Then by the truth of the marketing slogan, we infer ¬boughtAtSMM. But this contradicts boughtAtSMM (that is, from ¬boughtAtSMM and boughtAtSMM together we can prove that false is true). The problem must have been our pessimistic assumption payFull; clearly that couldn't have been true, and we're happy to know that ¬payFull.

Example 2.17

Spot the proof-by-contradiction used in The Simpsons:
Bart, fling through the school records: " Hey, look at this: Skinner makes $25,000 per year! "
Other kids: "Ooooh!"
Milhouse: "And he's 40 years old; that makes him a millionaire! "
Skinner, indignantly: " I wasn't a principal when I was 1!"
Milhouse: "And, he paints houses during the summer ... he's a billionaire!"
Skinner: "If I were a billionaire, would I still be living with my mother? " [Kids' laughter]
Skinner, to himself: " The kids just aren't responding to logic anymore! "

In the particular set of inference rules we have chosen to use, RAA is surprisingly important. It is the only way to prove formulas that begin with a single "¬".

Example 2.18

We'll prove 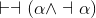$\vdash \dashv (\alpha\wedge \dashv \alpha)$

	$subproof:a\ \wedge \dashv a \vdash false$
1.a		α ∧ ¬α	Premise for subproof
1.b		α	∧Elim (left), line 1.a, where φ = α, and ψ = ¬α
1.c		¬α	∧Elim (right), line 1.a, where φ = α, and ψ = ¬α
1.d		false	falseIntro, lines 1.b,1.c, where φ = α
2	¬ (α ∧ ¬α)		RAA, line 1, where φ = α ∧ ¬α

Exercise 2.4.2.1

Here's another relatively simple example which uses RAA. Show that the modus tollens rule holds:
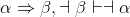
$\alpha\Rightarrow \beta,\dashv \beta\vdash \dashv \alpha$

Another use of subproofs is to organize proofs' presentations. Many proofs naturally break down into larger subparts, each with its own intermediate conclusion. These steps between these subparts are big enough to correspond to our intuition, but too big to correspond to individual inference rules. This gives additional useful structure to a proof, aiding our understanding.

Example 2.19

Previously, we showed that ∧ (AND) commutes (Example 2.14). However, that conclusion is only directly applicable when the ∧ is at the "top-level", i.e., not nested inside some other connective. Here, we'll show that ∧ commutes inside ¬, or more formally, 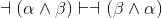$\dashv (\alpha\wedge \beta)\vdash \dashv (\beta\wedge \alpha)$

Caution: When doing inference-style proofs, we will not use the Boolean algebra laws nor replace subformulas with equivalent formulas. Conversely, when doing algebraic proofs, don't use inference rulesl While theoretically it's acceptable to mix the two methods, for homeworks we want to make sure you can do the problems using either method alone, so keep the two approaches separate!

We'll do two proofs of this to illustrate that there's always more than one way to prove something!

In our first proof, we'll use RAA. Why? Looking at our desired conclusion, what could be the last inference rule used in the proof to reach the conclusion? By the shape of the formula, the last step can't use any of the "introduction" inference rules (∧Intro, ∨Intro, ⇒Intro, falseIntro, or ¬Intro). We could potentially use any of the "elimination" inference rules. But, for ∧Elim, ∨Elim, ⇒Elim, ¬Elim, or CaseElim, we would first have to prove some more complicated formula to obtain our desired conclusion. That seems somewhat unlikely or unnecessary. For falseElim, we'd have to first prove false, i.e., obtain a contradiction, but our only premise isn't self-contradictory. The only remaining option is RAA.

1	¬ (α ∧ β)		Premise
2	subproof: $\beta \wedge \alpha\vdash false$
2.a		β ∧ α	Premise for subproof
2.b		α ∧ β	Theorem: ∧ commutes (Example 2.14), line 2a
2.c		false	falseIntro, lines 1,2.b
3	¬ (α ∧ β)		RAA, line 2

The proof above uses a subproof because it is necessary for the use of RAA. In contrast, the proof below uses two subproofs simply for organization.

For our second proof, let's not use RAA directly. Our plan is as follows:

Assume the premise ¬ (α ∧ β).
Again, use commutativity to show that β ∧ α ⇒ α ∧ β
Use modus tollens (Exercise 2.4.2.1) to obtain the conclusion.

We can organize the proof into corresponding subparts:

1	¬ (α ∧ β)		Premise
2	subproof:β ∧ α ⇒ α ∧ β
2.a		$\beta\wedge \alpha\vdash \alpha\wedge \beta$	Theorem statement: ∧ commutes (Example 2.14)
2.b		$\beta\wedge \alpha\Rightarrow \alpha\wedge \beta$	⇒Intro, line 2.a
3	subproof:¬ (β ∧ α)
3.a		$\beta\wedge \alpha\Rightarrow \alpha\wedge \beta,\dashv (\alpha\wedge \beta)\vdash \dashv (\beta\wedge \alpha )$	Theorem statement: modus tollens (Exercise 2.4.2.1)
3.b		$(\beta\wedge \alpha\Rightarrow \alpha\wedge \beta)\wedge \dashv (\alpha\wedge \beta)\Rightarrow (\beta\wedge \alpha )$	⇒Intro, line 3.a
3.c		$(\beta\wedge \alpha\Rightarrow \alpha\wedge \beta)\wedge \dashv (\alpha\wedge \beta)$	∧Intro, lines 2,1
3.d		$\dashv (\beta\wedge \alpha )$	⇒Elim, lines 3.b,3.c

2186 reads

You are here

Subproofs