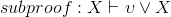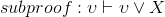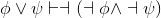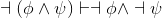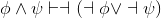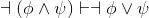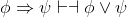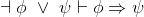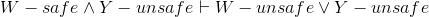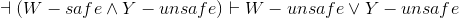For proofs on this homework, remember that each step must be justified by one of the following:
- a premise,
- a WaterWorld axioms (The domain axioms),
- a listed inference rule (Propositional inference rules) with the referenced line numbers (and, if ambiguous, substitutions for the inference rule's meta-variables), or
- a subproof shown inline, or equivalently, a theoremjlemma shown previously.
Except where otherwise directed, you may use any theorem shown in the text or by a previous exercise, even if that exercise was not assigned.
Exercise 2.6.1
Fill in the blank reasons in the following proof that ∨ commutes, that is, 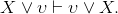
|
1 |
χ ∨ υ |
Premise |
|
|
2 |
|
||
|
2.a |
χ |
Premise for subproof |
|
|
2.b |
υ ∨ χ |
∨Intro, line 2.a |
|
|
3 |
|
||
|
3.a |
υ |
Premise for subproof |
|
|
3.b |
υ ∨ χ |
||
|
4 |
υ ∨ χ |
||
Exercise 2.6.2
Show that 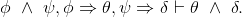
Exercise 2.6.3
Show what is often called the implication chain rule:
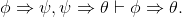
Exercise 2.6.4
Show what is often called negated-or-elimination (left):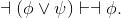
Exercise 2.6.5
Using the inference rule RAA, prove
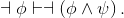
Exercise 2.6.6
Show that
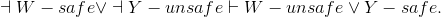
Exercise 2.6.7
In our inference rules, unlike our equivalences, we chose to not include any corresponding to distributivity.
- Prove a left-hand version of one direction of distributivity:
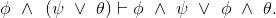
- Use the previous part's result, plus ∧'s commutativity to prove the corresponding right-hand version:
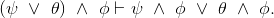
Exercise 2.6.8
In our inference rules, unlike our equivalences, we chose to not include any corresponding to DeMorgan's Law. Show that each of the following versions is still provable.
Exercise 2.6.9
The above exercise suggests that it would be useful to have an inference rule or theorem that says given 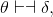 then
then 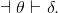 Or, equivalently, because of ⇒Intro and ⇒Elim,
Or, equivalently, because of ⇒Intro and ⇒Elim, 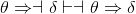
Why don't we?
Exercise 2.6.10
In our inference rules, unlike our equivalences, we have nothing that directly equates φ ⇒ ψ and ¬φ ∨ ψ. Prove each of the following.
Exercise 2.6.11
Prove the following: 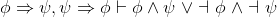
Exercise 2.6.12
Prove what is commonly called the Law of Excluded Middle: 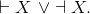
- Give a short proof citing our previous proof (Example 2.18) of
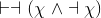 and the relevant version of DeMorgan's Law from above (Exercise 2.6.8).
and the relevant version of DeMorgan's Law from above (Exercise 2.6.8).
- Give a direct version without using previous theorems.
Exercise 2.6.13
Prove the missing steps and reasons in the following WaterWorld proof of 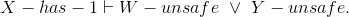
|
1 |
X − has − 1 |
||
|
2 |
WaterWorld axiom |
||
|
3 |
⇒Elim, lines 1,2 |
||
|
4 |
subproof: |
||
|
4.a |
W − safe ∧ Y − unsafe |
Premise for subproof |
|
|
4.b |
Y − unsafe |
||
|
4.c |
W − unsafe ∨ Y − unsafe |
||
|
5 |
subproof: |
||
|
5.a |
¬ (W − safe ∧ Y − unsafe) |
e)Premise for subproof |
|
|
5.b |
W − unsafe ∧ Y − safe |
CaseElim (left), lines where φ = |
|
|
5.c |
|||
|
5.d |
W − unsafe ∨ Y − unsafe |
||
|
6 |
W − safe ∧ Y − unsafe ∨ ¬ (W − safe ∧ Y − unsafe) |
Theorem: Excluded Middle, where χ = |
|
|
7 |
W − unsafe ∨ Y − unsafe |
||
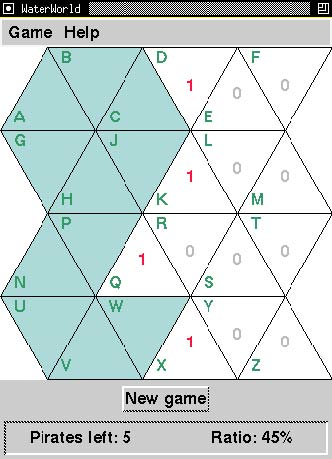
Given the above fgure (Figure 2.8), and using any of the immediately obvious facts as premises, prove that location P is safe by using our proof system and the WaterWorld axioms.
While this proof is longer (over two dozen steps), it's not too bad when sub-proofs are used appropriately. To make life easier, you may use the following theorem: Q −has − 1 ⇒ P − safe ∧ R − safe ∨ P − safe ∧ W − safe ∨ R − safe ∧ W − safe, along with any proven previously. When looking at the given board, you can use premises like Y − safe as well as ¬Y − unsafe.
Exercise 2.6.15
Starting from the WaterWorld axiom Q − has − 1 ⇒ P − safe ∧
R − safe ∧ W − unsafe ∨ P − safe
∧ R − unsafe ∧ W − safe ∨ P −
unsafe ∧ R − safe ∧ W − safe, we could prove the following theorem cited in the previous problem
(Exercise 2.6.14): Q − has − 1
⇒ P − safe ∧ R − safe ∨ P −
safe ∧ W − safe ∨ R − safe ∧ W
− safe.
Prove the following theorem which is slightly simpler: 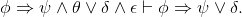
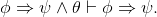
Exercise 2.6.16
Show that the ¬Elim inference rule is redudant in our system. In other words, with out using ¬Elim, prove that 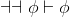
Exercise 2.6.17
Show that the ¬Intro inference rule is redundant in our system. In other words, without using ¬Intro, prove that
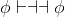 . To make sure that you're not hiding any uses of
¬Intro, also do not use any previous theorems.
. To make sure that you're not hiding any uses of
¬Intro, also do not use any previous theorems.
Exercise 2.6.18
Show that the CaseElim inference rule is redundant in our system. For brevity, we'll just consider the left-hand version. In other words, without using CaseElim, prove that 
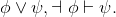 To make sure that you're not hiding any uses of CaseElim, also do not use any previous theorems.
To make sure that you're not hiding any uses of CaseElim, also do not use any previous theorems.
Exercise 2.6.19
- State where on a board pirates could be positioned, so that: P − has − 1 ∧ U − has − 1 ∧ W − has − 1, but X − safe.
- Compare this with a previous theorem (Example 2.22), B − has − 1 ∧ G − has − 1 ∧
- J − has − 1 ⇒ K − unsafe, the same idea shifted down a couple of rows. Suppose we try to translate this theorem's proof so as to conclude ¬X − safe (clearly untrue, by the above). What is the first step of the modifed proof which doesn't hold when B,G,J,Kare mindlessly replaced with P ,U,W ,X, respectively? (Just give a line number; no explanation needed. Your answer will be of the form "Lemma A line 1" or "main proof line 2".)
- We've just seen that the mindless changing of location-names introduces false steps. But we can be a little smarter, and modify the false step to get a formula which is true, and is also still in the spirit of the original proof. We can thus patch the problem from the previous part, and continue on modiflying the original proof for several more steps. But clearly we can't translate the entire original proof; we eventually hit a more fundamental snag: a formula which isn't true, yet can't be patched up, either. What is the first line that can't be patched? (Again, just give a line number; no explanation needed. Your answer will be of the form "Lemma A line 1" or "main proof line 2".)
Exercise 2.6.20
Which is worse, having an unsound (but complete) inference system or an incomplete (but sound) one? Why?
- 5851 reads