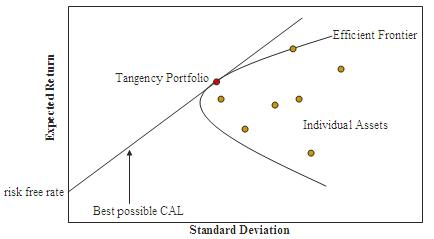
As shown in this graph, every possible combination of the risky assets, without including any holdings of the risk-free asset, can be plotted in risk-expected return space, and the collection of all such possible portfolios defines a region in this space. The left boundary of this region is a hyperbola 1, and the upper edge of this region is the efficient frontier in the absence of a risk-free asset (sometimes called "the Markowitz bullet"). Combinations along this upper edge represent portfolios (including no holdings of the risk-free asset) for which there is lowest risk for a given level of expected return. Equivalently, a portfolio lying on the efficient frontier represents the combination offering the best possible expected return for given risk level.
Matrices are preferred for calculations of the efficient frontier.
In matrix form, for a given "risk tolerance" 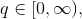 , the efficient
frontier is found by minimizing the following expression:
, the efficient
frontier is found by minimizing the following expression:
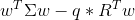
where
w is a vector of portfolio weights and 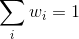 . (The weights can be negative,
which means investors can short a security.);
. (The weights can be negative,
which means investors can short a security.);
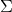 is the covariance matrix for the returns on the assets in the portfolio;
is the covariance matrix for the returns on the assets in the portfolio;
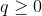 is a "risk tolerance" factor, where 0 results in the portfolio with minimal
risk and
is a "risk tolerance" factor, where 0 results in the portfolio with minimal
risk and 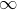 results in the portfolio infinitely far out on the frontier with
both expected return and risk unbounded; and
results in the portfolio infinitely far out on the frontier with
both expected return and risk unbounded; and
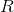 is a vector of expected returns.
is a vector of expected returns.
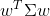 is the variance of portfolio return.
is the variance of portfolio return.
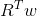 is the expected return on the portfolio.
is the expected return on the portfolio.
The above optimization finds the point on the frontier at which the inverse of the slope of the frontier would be q if portfolio return variance instead of standard deviation were plotted horizontally. The frontier in its entirety is parametric on q.
Many software packages, including MATLAB, Microsoft Excel, Mathematica and R, provide optimization routines suitable for the above problem.
An alternative approach to specifying the efficient frontier is to do so parametrically on the expected portfolio return 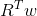 . This version of the problem requires that we minimize
. This version of the problem requires that we minimize
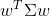
subject to
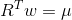
for parameter 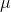 . This problem is easily solved using a Lagrange multiplier.
. This problem is easily solved using a Lagrange multiplier.
- 14397 reads






