The asset return depends on the amount paid for the asset today. The price paid must ensure that the market portfolio's risk / return characteristics improve when the asset is added to it. The CAPM is a model which derives the theoretical required expected return (i.e., discount rate) for an asset in a market, given the risk-free rate available to investors and the risk of the market as a whole. The CAPM is usually expressed:
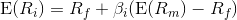
\beta , Beta, is the measure of asset sensitivity to a movement in the overall market; Beta is usually found via regression on historical data. Betas exceeding one signify more than average "riskiness" in the sense of the asset's contribution to overall portfolio risk; betas below one indicate a lower than average risk contribution.
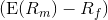 is the market premium, the expected excess return of
the market portfolio's expected return over the risk-free rate.
is the market premium, the expected excess return of
the market portfolio's expected return over the risk-free rate.
This equation can be statistically estimated using the following regression equation:
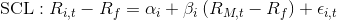
where αi is called the asset's alpha, βi is the asset's beta coefficient and SCL is the Security Characteristic Line.
Once an asset's expected return, 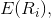 is calculated using CAPM, the future cash
flows of the asset can be discounted to their present value using this rate to establish the correct price for the asset. A riskier stock will have a higher beta and will be discounted at a
higher rate; less sensitive stocks will have lower betas and be discounted at a lower rate. In theory, an asset is correctly priced when its observed price is the same as its value calculated
using the CAPM derived discount rate. If the observed price is higher than the valuation, then the asset is overvalued; it is undervalued for a too low price.
is calculated using CAPM, the future cash
flows of the asset can be discounted to their present value using this rate to establish the correct price for the asset. A riskier stock will have a higher beta and will be discounted at a
higher rate; less sensitive stocks will have lower betas and be discounted at a lower rate. In theory, an asset is correctly priced when its observed price is the same as its value calculated
using the CAPM derived discount rate. If the observed price is higher than the valuation, then the asset is overvalued; it is undervalued for a too low price.
(1) The incremental impact on risk and expected return when an additional risky asset, a, is added to the market portfolio, m, follows from the formulae for a two-asset portfolio. These results are used to derive the asset-appropriate discount rate.
Market portfolio's risk = ![(w_m^2 \sigma_m ^2 + [ w_a^2 \sigma_a^2 + 2 w_m w_a \rho_{am} \sigma_a \sigma_m] )](/system/files/resource/12/12158/12440/media/eqn-img_5.gif)
Hence, risk added to portfolio = ![[ w_a^2 \sigma_a^2 + 2 w_m w_a \rho_{am} \sigma_a \sigma_m]](/system/files/resource/12/12158/12440/media/eqn-img_6.gif)
but since the weight of the asset will be relatively low, 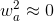
i.e. additional risk = ![[ 2 w_m w_a \rho_{am} \sigma_a \sigma_m] \quad](/system/files/resource/12/12158/12440/media/eqn-img_8.gif)
Market portfolio's expected return = ![( w_m \operatorname{E}(R_m) + [ w_a \operatorname{E}(R_a) ] )](/system/files/resource/12/12158/12440/media/eqn-img_9.gif)
Hence additional expected return = ![[ w_a \operatorname{E}(R_a) ]](/system/files/resource/12/12158/12440/media/eqn-img_10.gif)
(2) If an asset, a, is correctly priced, the improvement in its risk-to-expected return ratio achieved by adding it to the market portfolio, m, will at least
match the gains of spending that money on an increased stake in the market portfolio. The assumption is that the investor will purchase the asset with funds borrowed at the risk-free rate,
 ; this is rational if
; this is rational if 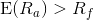 .
.
Thus: ![[ w_a ( \operatorname{E}(R_a) - R_f ) ] / [2 w_m w_a \rho_{am} \sigma_a \sigma_m] = [ w_a ( \operatorname{E}(R_m) - R_f ) ] / [2 w_m w_a \sigma_m \sigma_m ]](/system/files/resource/12/12158/12440/media/eqn-img_13.gif)
i.e. : ![[\operatorname{E}(R_a) ] = R_f + [\operatorname{E}(R_m) - R_f] * [ \rho_{am} \sigma_a \sigma_m] / [ \sigma_m \sigma_m ]](/system/files/resource/12/12158/12440/media/eqn-img_14.gif)
i.e. : ![[\operatorname{E}(R_a) ] = R_f + [\operatorname{E}(R_m) - R_f] * [\sigma_{am}] / [ \sigma_{mm}]](/system/files/resource/12/12158/12440/media/eqn-img_15.gif)
![[\sigma_{am}] / [ \sigma_{mm}] \quad](/system/files/resource/12/12158/12440/media/eqn-img_16.gif) is the "beta",
is the "beta", 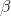 return— the covariance between the asset's return and the market's return divided by the variance of
the market return— i.e. the sensitivity of the asset price to movement in the market portfolio's value.
return— the covariance between the asset's return and the market's return divided by the variance of
the market return— i.e. the sensitivity of the asset price to movement in the market portfolio's value.
- 3048 reads






