You are here

Home » MATH S121 A Foundation In Pure Mathematics (Free Courseware) » Counting and Basic Probability » Counting

Addition Principle

3 June, 2015 - 16:54
Available under Creative Commons-ShareAlike 4.0 International License.

Let's look at a simple counting problem.

Example 1

Given a small set of numbers denoted by A = {-4, -2, 1, 3, 5, 6, 7, 8, 9, 10}, it is easy to see that there are a total of 10 numbers in A.

Now, if we are interested in determining the number of elements of the events E1, E2, and E, which are defined as:

  • E1 = choosing a negative number from A
  • E2 = choosing an odd number from A
  • E = choosing a negative or an odd number from A.

Apply the Addition Principle to determine the number of outcomes of events E using E1 and E2.

Solution

E1 = {-4, -2}, and the number of outcomes for E1 is n(E1) = 2.

E2 = {1, 3, 5, 7, 9}, and the number of outcomes for E2 is n(E2) = 5.

Events E1 and E2 are mutually exclusive because there is no common outcomes in the list of E1 and E2. So the number of outcomes of event E is

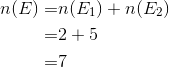
\begin{align*} n(E) =& n(E_{1}) + n(E_{2})\\ =& 2 + 5\\ =&7 \\ \end{align*}

This answer can be confirmed if we can list out all the elements of E. In this example the outcomes of E is

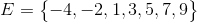
E = \begin{Bmatrix} -4, -2, 1, 3, 5, 7, 9 \end{Bmatrix}

This gives n(E) = 7, which is the same answer as above.

Addition Principle

For a series of mutually exclusive events E1, E2, E3,. . . ,En, and each event, say Ei has n(Ej) outcomes regardless of the process made on the previous events.

Then, the total number of possible outcomes is given by

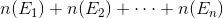
n(E_{1}) + n(E_{2}) + \cdots + n(E_{n})

Example 2

In how many ways can a number be chosen from the set

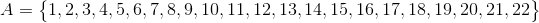
A =\begin{Bmatrix} 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 \end{Bmatrix}

such that

a. it is a multiple of 3 or 8?
b. it is a multiple of 2 or 3?
 

Solution

a. Let E1 = multiples of 3:
    E1 = {3, 6, 9, 12, 15, 18, 21}, so n(E1) = 7.
  Let E2 = multiples of 8:
    E2 = {8, 16}, so n(E2) = 2.
  Events E1 and E2 are mutually exclusive, so
    n(E) = n(E1) + n(E2) = 7+2 = 9
b. Let E1 = multiples of 2:
    E1 = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22}, so n(E1) = 11.
  Let E2 = multiples of 3:
    E2 = {3, 6, 9, 12, 15, 18, 21}, so n(E2) = 7.
The events E1 and E2 are not mutually exclusive since they contain the same elements {6, 12, 18}. If the problem involves events that are not mutually exclusive, we can handle the counting as follows:
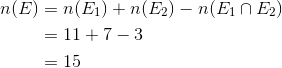
\begin{align*} n(E)&=n(E_{1})+n(E_{2})-n(E_{1}\cap E_{2})\\ &= 11+7- 3\\ &= 15\\ \end{align*}
where E1 ∩ E2 means 'the intersection of the sets E1 and E2'.
 
  • 960 reads