We have all faced the scenario where we've had to decide between two choices such as: do you go to the cinema with friends or do you read this module? Sometimes when you can't make the decision you opt to let 'lady luck' decide.
Animation/activity
| Let's say you pull out a fair $1-coin and assign one option to each side: | |
|
'flower' = go to cinema '1' = read the module |
|
| You toss the fair coin and whichever side lands on top will be your choice. This method gives an even chance that either side will land on top, so either option is equally possible. Try 'tossing' the virtual coin here at least 10 times, or more. | |
|
|
|
| However, just before you toss the coin, your mother calls asking you to come over for a meal. Now you have three choices, but your coin only has two sides. Assigning a meal with your mother to the coin landing on its edge and balancing there hardly seems fair! Therefore, you come up with the following plan: you take out a second fair $1-coin and decide to toss both coins; you assign the following results to your choices | |
|
'flower' + 'flower' = go to cinema 'flower' + '1' = read the module '1' + '1' = meal with mother |
|
| Now let's say you 'toss' the two coins together, | |
|
|
|
| You used two coins in the belief that each of the three options has the same chance of been chosen. But has it? | |
You should now have your own results from your 'virtual coin toss'. Let's assume I tried the same exercise, and that I also used two fair coins.
Here are my results from tossing my two coins 50 times:
| No. of times | % | |
|---|---|---|
| 'flower' + 'flower' | 10 | 20 |
| 'flower' + '1' | 27 | 54 |
| '1' + '1' | 13 | 26 |
This hardly looks like the three options are evenly distributed! We might expect some small variation, but not as much as 54% for one option!
The problem with tossing the two coins comes from poor counting of the outcomes. Let's consider a different situation for the moment.
Example 7
For the set
A = {a,b}
how many different combinations of the two elements in A are there if repetition is allowed, and order is important?
Solution
Step 1: there are two ways of choosing the first element.
Step 2: there are two ways of choosing the second element.
The Multiplication Principle gives a total of
2 × 2 = 4
different ways, and they are:
aa
ab
ba
bb
So now let's reconsider your tossing two fair coins one by one. As in the example, we could get four possible outcomes:
| First coin | Second coin |
|---|---|
| Flower | Flower |
| Flower | 1 |
| 1 | Flower |
| 1 | 1 |
But - you may say - the second and third outcomes are the same!
In fact, they are not the same.
The first result in each outcome refers to the first coin, and the second result refers to the second coin. Therefore, each outcome represents a unique outcome.
The confusion arises because we originally assumed that the second and third outcomes represented the same choice. Thus, the second option, i.e. to 'read the module', is twice as likely to appear on a toss of the coins, which explains the results of our experiment.
To further demonstrate the fact that there are four outcomes, suppose we had to decide between the four choices: go to the cinema, read the module, meal with mother and sleep. We arrange to toss two fair coins. However, this time we toss the first coin to our left and the second coin to our right and record the result differently. This gives us four different outcomes:
| Left coin | Right coin |
|---|---|
| 'flower' | 'flower' |
| 'flower' | '1' |
| '1' | 'flower' |
| '1' | '1' |
We can assign these to our four different choices comfortable in the knowledge that each outcome is equally likely.
In mathematics we don't talk about chances, but about probabilities. As you saw in our last example, counting forms an essential part of determining the probability of each outcome. There are four outcomes, each of which is equally likely. We define the probability of each outcome as one chance in four outcomes, or:
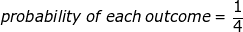
Example 8
Each suit contains 13 cards, and there are 52 cards in total. Assuming that the pack has been well shuffled, then the probability that the top card is of one particular suit is the same as the probability that it is of any of the other suits, or:

Let's look at the last example more closely. If we are looking for a club, then when we turn over the top card success is measured by the card being any one of
{Ace♣,2♣,3♣,4♣,5♣,6♣,7♣,8♣,9♣,10♣,Jack♣,Queen♣,King♣}.
That is, when turning over the top card, there are 13 possible successful outcomes out of the total of 52 possible outcomes.
An important feature of the last example is that there is an equal chance that each card in the pack could be at the top. The position of the cards in a shuffled pack is considered to be random, i.e. there is no way of predicting which card will be in which position. Similarly, with our tossing the coin example the result of the toss is random as there is no way of knowing which side will appear on top after each toss.
Example 9
In a race at Happy Valley, there are ten horses running. Are the chances that any horse wins the same?
Solution
No. There are many different factors determining the winner of a horse race - the skill of the jockey, the state of the track, the training of the horse, etc.
Example 10
On a roulette wheel there are 38 equal divisions. Two divisions are numbered zero, and the rest are numbered from one to 36. Gamblers are allowed to bet on the ball landing in any of the divisions numbered one to 36. If the ball lands in one of the divisions marked '0', then the casino wins all bets. Are the chances that the ball will indicate any of the numbers zero to 36 the same?
Solution
No. Since there are two divisions marked '0' and only one for each of the other numbers, then the chances of landing on a '0' will be greater than for any of the other numbers.
- 1458 reads






