You are here

Home » MATH S121 A Foundation In Pure Mathematics (Free Courseware) » Counting and Basic Probability » Counting » Permutations and combinations » Activity 2

Activity 2 feedback

23 November, 2015 - 16:52
Available under Creative Commons-ShareAlike 4.0 International License.
  1. Choose 3 from 9, since the eldest boy is fixed. The number of different ways is

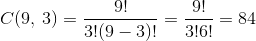
C(9,\:3)=\frac{9!}{3!(9-3)!}=\frac{9!}{3!6!}=84

  1. If the eldest boy is excluded, we actually choose 4 boys from 9. The number of different ways is

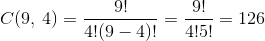
C(9,\:4)=\frac{9!}{4!(9-4)!}=\frac{9!}{4!5!}=126

  1. The number of all possible groups is

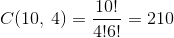
C(10,\:4)=\frac{10!}{4!6!}=210

So the proportion of all possible groups containing the eldest boy is:

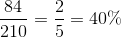
\frac{84}{210}=\frac{2}{5}=40\%

  1. Choose 3 from 9, since the eldest boy is fixed. The number of different ways is

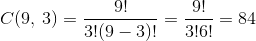
C(9,\:3)=\frac{9!}{3!(9-3)!}=\frac{9!}{3!6!}=84

  1. If the eldest boy is excluded, we actually choose 4 boys from 9. The number of different ways is

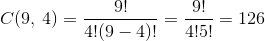
C(9,\:4)=\frac{9!}{4!(9-4)!}=\frac{9!}{4!5!}=126

  1. The number of all possible groups is

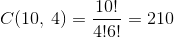
C(10,\:4)=\frac{10!}{4!6!}=210

So the proportion of all possible groups containing the eldest boy is:

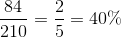
\frac{84}{210}=\frac{2}{5}=40\%

We have all faced the scenario where we've had to decide between two choices such as: do you go to the cinema with friends or do you read this module? Sometimes when you can't make the decision you opt to let 'lady luck' decide.

  • 741 reads