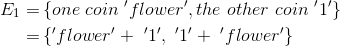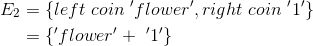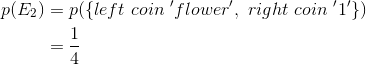The probability of one event

Available under Creative Commons-ShareAlike 4.0 International License.

In order to investigate probabilities mathematically, we need to ensure that we have unambiguous definitions and terminology for describing problems. We start by identifying the scope of a problem.

Definition 1: An experiment is a process that yields an outcome.

Definition 2: An event, E, is an outcome or combination of outcomes from an experiment.

Definition 3: A sample space, S, is the event consisting of all possible outcomes.

Example 11

In the single toss of a fair coin, we assume the 'flower' represents 'the side on top after the toss is the flower', etc.

The sample space is: S = {'flower', '1'}

And one event is: E₁ = {'flower'}

Another event is: E₂ = {'1'}

Example 12

In the single toss of two fair coins:
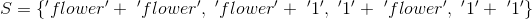
	$S = \left \{ 'flower' +\ 'flower',\ 'flower' +\ '1',\ '1' +\ 'flower',\ '1' +\ '1' \right \}$
And one event is:
	$\begin{align} E_{1} =& \left \{ one\ coin\ 'flower', the\ other\ coin\ '1' \right \}\\ =& \left \{ 'flower' +\ '1',\ '1' +\ 'flower' \right \} \\ \end{align}$
Another event is:
	$\begin{align} E_{2} &= \left \{ left\ coin\ 'flower', right\ coin\ '1' \right \} \\ &= \left \{ 'flower' +\ '1' \right \}\\ \end{align}$
E₁ and E₂ are therefore very different events, as you saw earlier.

Example 13

For the pack of cards example:

If E₁ is the event that the top card is a club, then this is the subset:

E₁ = {Ace♣,2♣,3♣,4♣,5♣,6♣,7♣,8♣,9♣,10♣,Jack♣,Queen♣,King♣}

For the event that the top card is a face card, then:

Definition 4: If S is a finite sample space in which all outcomes are equally likely, and E is an event in S, then the probability of E is:

$p(E)=\frac{number\:of\:outcomes\:in\:E}{total\:number\:of\:outcomes\:in\:S}$

Or, if we define a 'successful outcome' as one in E, then:

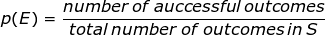
$p(E)= \frac{number\:of\:auccessful\:outcomes}{total\:number\;of\:outcomes\:in\:S}$

Example 14

In a single toss of a fair coin there is one 'successful outcome' in both E₁ and E₂ and two outcomes in S. Therefore:

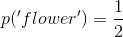
$p('flower') = \frac{1}{2}$

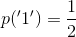
$p('1') = \frac{1}{2}$

Example 15

In the single toss of two fair coins independently, there are four outcomes in S. Therefore:

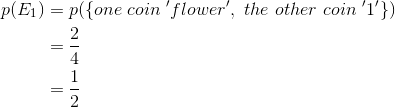
$\begin{align*} p(E_{1})&=p({\left \{ one\ coin\ 'flower',\ the\ other\ coin\ '1' \right \}})\\ &=\frac{2}{4}\\ &=\frac{1}{2}\\ \end{align*}$

And for:

$\begin{align*} p(E_{2})&=p({\left \{ left\ coin\ 'flower',\ right\ coin\ '1' \right \}})\\ &=\frac{1}{4}\\ \end{align*}$

Example 16

In investigating the value of the top card of a shuffled pack, S contains 52 possible outcomes. For the top card to be a club, then there are 13 'successful outcomes', so:

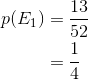
$\begin{align*} p(E_{1}) &=\frac{13}{52} \\ &= \frac{1}{4}\\ \end{align*}$

For the top card to be a face card, there are 20 'successful outcomes', so:

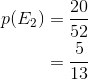
$\begin{align*} p(E_{2}) &=\frac{20}{52} \\ &=\frac{5}{13}\\ \end{align*}$

As you can now see, for many problems, such as tossing two coins, the difficulties arise in accurately identifying the outcomes.

A roulette wheel is a common tool for gambling in casinos and knowledge of how probabilities apply is essential for the educated gambler. The wheel contains pockets at its edge large enough to hold the ball that forms part of the equipment. Each hole is labelled with a number, and is coloured either black or red. At the start of each play gamblers must place a bet on a number, group of numbers or colour. The wheel is then spun in one direction and the ball is made to travel in the opposite direction in a slot above the wheel. Once the speed of the ball drops to a point where it can no longer stay in the slot it falls onto the wheel where it bounces around until it settles into one of the pockets to determine the winning number and colour. Usually the casino will reserve the slot numbered '0' for itself - when the ball lands in that slot the casino wins all bets. When the ball lands on any other number the payout is normally related to the associated probability.

Example 17

For a roulette wheel with two zeros, if we denote the two zeros as separate outcomes '01' and '02', then S has 38 different outcomes, which are all equally likely:

and if we interested in the probability of the ball landing on the '8', then:

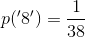
$p('8') =\frac{1}{38}$

Note, however:

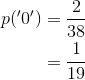
$\begin{align*} p('0') &=\frac{2}{38}\\ &=\frac{1}{19}\\ \end{align*}$

If you think that the 'house advantage' built into roulette makes little difference, try the Internet activity.

In addition to coins, cards and roulette wheels, another common device that appears in games of chance is the die (the more familiar plural is 'dice'). By a 'fair dice' we mean that there is an equal probability of any of the six sides appearing at the top after a throw.

Example 18

Let E_i be the event when the die ends with the side showing the value i at the top (i=1,2,3,4,5,6), then:

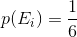
$p(E_{i}) = \frac{1}{6}$

Games with dice become more interesting when more than one die is involved. Such games are normally based on the combined values of the sides appearing on top after a throw.

Example 19

What is the probability of the total of the top sides of two dice being 10?

Solution

First of all, let's calculate the size of our sample space. As each die has 6 sides and the result on one die is not dependent on the other we can use the Multiplication Principle to determine that there are 6 × 6 = 36 possible combinations, presented here as ordered pairs to indicate the values of the first and second die:

(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6), 　
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6), 　
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)

These possibilities generate the following 36 totals:

2,3,4,5,6,7,3,4,5,6,7,8, 　
4,5,6,7,8,9,5,6,7,8,9,10, 　
6,7,8,9,10,11,7,8,9,10,11,12

We can see that there are three possible outcomes that generate a total of 10: (4,6),(5,5),(6,4) giving:

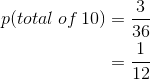
$\begin{align*} p(total\:of\:10) &=\frac{3}{36}\\ &=\frac{1}{12}\\ \end{align*}$

In the previous example, it was crucial that we handled the possible outcomes as ordered pairs to ensure that we capture the two successful outcomes (4,6) and (6,4).

Example 20

One game with dice is based on the player throwing two dice and obtaining a total of 8 or greater. What is the probability of the player winning?

Solution

There are 15 successful outcomes:

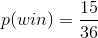
$p(win) = \frac{15}{36}$

As you can see, the possibility of winning is less than 50%.

Probabilities are also used extensively in quality control especially in production lines.

Example 21

A company manufacturers computer circuit boards. The process produces 20 defective boards in every 1000. In taking a sample of 5 from the 1000, what is the probability that the sample will contain no defectives?

Solution

Since order is not involved here, the selection of 5 boards relates to combinations. There are C(1000,5) ways of selecting the 5 boards - this is our sample space.

There are 980 non-defective boards, and there are C(980,5) ways of selecting 5 boards from these - these are our successful outcomes.

Therefore, the probability, to five decimal places, is:

$\begin{align*} p(no\:defectives\: in\: the\: sample) &= \frac{C(980,5)}{C(1000,5)}\\ &=0.90374\\ \end{align*}$

Most people in Hong Kong have participated at least once in the Mark Six lottery.

Example 22

What are the actual chances of winning the Mark Six?

Solution

Each play involves the drawing of 6 numbers from 49, and the order that the numbers are drawn is irrelevant. This means that there are C(49,6) possible outcomes - this is our sample space. There is only one winning combination, so:

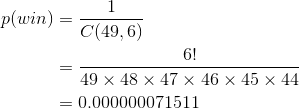
$\begin{align*} p(win)&=\frac{1}{C(49,6)}\\ &=\frac{6!}{49\times 48\times 47\times 46\times 45\times 44}\\ &=0.000000071511\\ \end{align*}$

850 reads

You are here

The probability of one event