You are here

Home » MATH S121 A Foundation In Pure Mathematics (Free Courseware) » Counting and Basic Probability » Counting

Multiplication Principle

19 January, 2016 - 14:05
Available under Creative Commons-ShareAlike 4.0 International License.

Suppose that two independent events E1 and E1 can result in n(E1) and n(E2) possible outcomes, respectively, and that there are no restrictions on choice.

The total number of different combinations of possible outcomes from E1 and E1 can then be determined by using the Multiplication Principle, that is

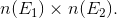
n(E_{1}) \times n(E_{2}).

Multiplication Principle

If a process can be performed in a series of independent successive events E1, E2, E3,. . . , En and each event, say Ei, can be completed in n(Ej) ways regardless of the process made on the previous events.

Then the total number of different combinations of completing the entire process is given by

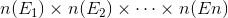
n(E_{1}) \times n(E_{2}) \times \cdots \times n(En)

Example 3

What is the total number of possible outcomes when you flip a fair coin twice?

Solution

Let T be the 'tail' and H be the 'head' of a fair coin. The events are:

  • E1 = first flip (2 possible outcomes: H or T, so n(E1)= 2)
  • E2 = second flip (2 outcomes: H or T, so n(E2) = 2)

The events are independent and that the flip does not affect the outcome of the other flip.

Hence the total number of possible outcomes is

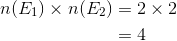
\begin{align*} n(E_{1}) \times n(E_{2}) &= 2 \times 2\\ &= 4 \\ \end{align*}

[We could also list the outcomes as: HH HT TH TT].

In the previous example, you can also model the 4 possible outcomes using a tree diagram or an outcome table, as shown below:

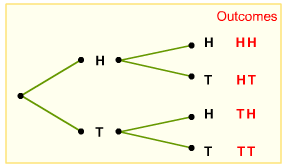
1st Flip

2nd Flip

Outcomes

Table 1.1 Tree diagram

H

H

HH

H

T

HT

T

H

TH

T

T

TT

Outcome Table

 

Example 4

The life insurance policies of an insurance company are classified by:

  • age of the insured: under 25 years, between 25 years and 50 years, over 50 years old;
  • sex: M or F; and
  • marital status: single or married.

What is the total number of classifications?

Solution

The events are:

Table 1.2  
E1 = age of the insured: 3 age divisions, so n(E1) = 3

E2 = sex:

2 possibilities of sex, so n(E2) = 2

E3 = marital status:

2 possibilities of martial status, so n(E3) = 2
 

All events E1, E2 and E3 are independent, so the total number of different classifications is

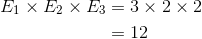
\begin{align*} E_{1} \times E_{2} \times E_{3} &= 3 \times 2 \times 2\\ &= 12\\ \end{align*}

  • 954 reads