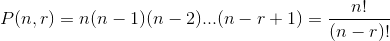A permutation is an arrangement of all or part of a set of n objects, with regard to the order of the arrangement and without repetition. That is, the order in which we arrange objects is important.
Notations for permutations
| 1. | The number of different arrangement of a set of n distinct objects is given by | |
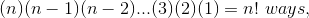
|
||
| where n! is called the 'n factorial'. | ||
| 2. | The number of permutations of a set of n distinct objects taken r at a time, denoted the permutation by P(n, r) or Prn, where repetitions are not allowed, is given by | |
|
|
||
| Note: P(n, r) = n! | ||
Example 5
Consider arranging 3 letters: A, B, C.
How many different ways can this be done, assuming that repetitions are not allowed?
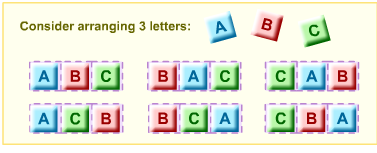
As you can see, there are 6 possible permutations if we have three letters, and no repetitions.
We can get the answer without listing out all the elements by using the permutation formula
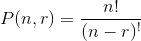
The number of different ways of a set of 3 distinct objects taken 3 at a time can be arranged without repetition is
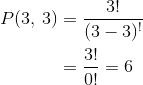
where 0! = 1.
- 2141 reads