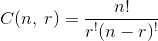What is a combination?
A combination is a selection of all or part of a set of n objects without repetition, and with regardless to the order in which objects are selected. That is, the order is not important.
For example, suppose you are asked to select a set of 4 different letters from the 26 English alphabet {A, B, C, D,. . . , Z} without regard to the order. Let's say you got
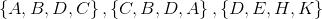
Actually, the set {A, B, D, C}, {C, B, D, A} have the same set of letters, even though the 4 letters are selected in different order. Hence, you have selected only two different sets of 4 letters (not 3 sets!).
Notations for combination
The number of combinations in which r objects can be selected from a set of n objects, where repetitions are not allowed and the ordering is not important, is denoted by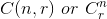
|
||
|
|
||
| Notes: | ||
| 1. |
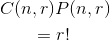
|
|
| 2. |
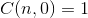
|
|
| 3. |
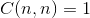
|
|
| 4. |
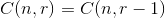
|
|
Example 6
How many different ways of 4 letters can be selected from the 26 alphabet when repetitions are not allowed and the ordering of letters is not important?
Solution
There are P(26, 4) ways of arranging any 4 letters chosen from the 26 alphabet without repetitions. We can apply the permutation to get
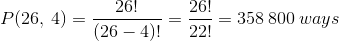
Since the order of any set of 4 letters chosen can be arranged in 4! different ways, the number of different sets of 4 letters is
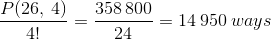
The same result can be obtained if you use the combination formula
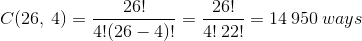
- 1572 reads