Exercise 6.4. Draw a stack diagram for the following program. What does the program print? Solution: http://www.greenteapress.com/thinkpython/code/stack_diagram.py .
def b(z):
prod = a(z, z)
print z, prod
return prod
def a(x, y):
x = x + 1
return x * y
def c(x, y, z):
total = x + y + z
square = b(total)**2
return square
x = 1
y = x + 1
print c(x, y+3, x+y)
Exercise 6.5. The Ackermann function, A(m, n), is defined:
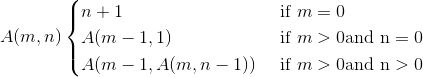
See https://en.wikipedia.org/wiki/Ackermann_function. Write a function named ackthat evaluates Ackermann’s function. Use your function to evaluate ack(3, 4), which should be 125. What happens for larger values of mand n? Solution: http://thinkpython.com/code/ackermann.py.
Exercise 6.6. A palindrome is a word that is spelled the same backward and forward, like “noon” and “redivider”. Recursively, a word is a palindrome if the first and last letters are the same and the middle is a palindrome.
The following are functions that take a string argument and return the first, last, and middle letters:
def first(word):
return word[0]
def last(word):
return word[-1]
def middle(word):
return word[1:-1]
We’ll see how they work in Strings .
- Type these functions into a file named palindrome.py and test them out. What happens if you call middle with a string with two letters? One letter? What about the empty string, which is written '' and contains no letters?
- Write a function called is_palindrome that takes a string argument and returns True if it is a palindrome and False otherwise. Remember that you can use the built-in function len to check the length of a string.
Solution: http://thinkpython.com/code/ paLindrome soLn.py.
Exercise 6.7. A number, a, is a power of b if it is divisible by b and a/b is a power of b. Write a function calledis_powerthat takes parameters a andb and returns Trueif a is a power of b. Note: you will have to think about the base case.
Exercise 6.8. The greatest common divisor (GCD) of a and b is the largest number that divides both of them with no remainder.
One way to find the GCD of two numbers is based on the observation that if r is the remainder when a is divided by b, then gcd(a, b)= gcd(b, r). As a base case, we can use gcd(a,0)= a.
Write a function called gcd that takes parameters a andb and returns their greatest common divisor.
Credit: This exercise is based on an example from Abelson and Sussman’sStructure and Interpretation of Computer Programs.
- 3859 reads






