We have only covered a small subset of Python, but you might be interested to know that this subset is a complete programming language, which means that anything that can be computed can be expressed in this language. Any program ever written could be rewritten using only the language features you have learned so far (actually, you would need a few commands to control devices like the keyboard, mouse, disks, etc., but that’s all).
Proving that claim is a nontrivial exercise first accomplished by Alan Turing, one of the first computer scientists (some would argue that he was a mathematician, but a lot of early computer scientists started as mathematicians). Accordingly, it is known as the Turing Thesis. For a more complete (and accurate) discussion of the Turing Thesis, I recommend Michael Sipser’s book Introduction to the Theory of Computation.
To give you an idea of what you can do with the tools you have learned so far, we’ll evaluate a few recursively defined mathematical functions. A recursive definition is similar to a circular definition, in the sense that the definition contains a reference to the thing being defined. A truly circular definition is not very useful:
vorpal: An adjective used to describe something that is vorpal.
If you saw that definition in the dictionary, you might be annoyed. On the other hand, if you looked up the definition of the factorial function, denoted with the symbol !, you might get something like this:
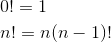
This definition says that the factorial of 0 is 1, and the factorial of any other value, n, is n multiplied by the factorial of n − 1.
So 3! is 3 times 2!, which is 2 times 1!, which is 1 times 0!. Putting it all together, 3! equals 3 times 2 times 1 times 1, which is 6.
If you can write a recursive definition of something, you can usually write a Python pro gram to evaluate it. The first step is to decide what the parameters should be. In this case it should be clear that factorial takes an integer:
def factorial(n):
If the argument happens to be 0, all we have to do is return 1:
def factorial(n):
if n == 0:
return 1
Otherwise, and this is the interesting part, we have to make a recursive call to find the factorial of n − 1 and then multiply it by n:
def factorial(n):
if n == 0:
return 1
else:
recurse = factorial(n-1)
result = n * recurse
return result
The flow of execution for this program is similar to the flow of countdown in Recursion. If we call factorial with the value 3:
Since 3 is not 0, we take the second branch and calculate the factorial of n-1...
Since 2 is not 0, we take the second branch and calculate the factorial of n-1...
Since 1 is not 0, we take the second branch and calculate the factorial of n-1...
Since 0 is 0, we take the first branch and return 1 without making any more recursive calls.
The return value (1) is multiplied by n, which is 1, and the result is returned.
The return value (1) is multiplied by n, which is 2, and the result is returned.
The return value (2) is multiplied by n, which is 3, and the result, 6, becomes the return value of the function call that started the whole process.
Return values shows what the stack diagram looks like for this sequence of function calls.
The return values are shown being passed back up the stack. In each frame, the return value is the value of result, which is the product of n and recurse.
In the last frame, the local variables recurse and result do not exist, because the branch that creates them does not execute.
 .
.
- 瀏覽次數:2870






