Exercise 7.3.To test the square root algorithm in this chapter, you could compare it with math.sqrt. Write a function named mtest_square_root that prints a table like this:
1.02.03.04.05.06.07.08.09.0 |
1.01.414213562371.732050807572.02.23606797752.449489742782.645751311062.828427124753.0 |
1.01.414213562371.732050807572.02.23606797752.449489742782.645751311062.828427124753.0 |
0.02.22044604925e-160.00.00.00.00.04.4408920985e-160.0 |
The first column is a number, a; the second column is the square root of a computed with the function from Square roots; the third column is the square root computed by math.sqrt; the fourth column is the absolute value of the difference between the two estimates.
Exercise 7.4.The built-in function eval takes a string and evaluates it using the Python interpreter. For example:
>>> eval('1 + 2 * 3')7>>> import math>>> eval('math.sqrt(5)')2.2360679774997898>>> eval('type(math.pi)')<type 'float'>
Write a function called eval_loopthat iteratively prompts the user, takes the resulting input and evaluates it using eval, and prints the result.
It should continue until the user enters 'done', and then return the value of the last expression it evaluated.
Exercise 7.5. The mathematician SrinivasaRamanujan found an infinite series that can be used to generate a
numerical approximation of 1/π:
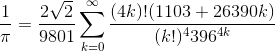
Write a function called estimate_pithat uses this formula to compute and return an estimate of π. It should use a whileloop to compute terms of the summation until the last term is smaller than 1e-15(which is Python notation for 10−15). You can check the result by comparing it to math.pi.
Solution: http://thinkpython.com/code/pi.py.
- 瀏覽次數:2636






