As you write larger functions, you might find yourself spending more time debugging.
To deal with increasingly complex programs, you might want to try a process called incremental development. The goal of incremental development is to avoid long debugging sessions by adding and testing only a small amount of code at a time.
As an example, suppose you want to find the distance between two points, given by the coordinates (x1, y1) and (x2, y2). By the Pythagorean theorem, the distance is:
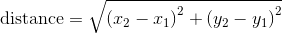
The first step is to consider what a distance function should look like in Python. In other words, what are the inputs (parameters) and what is the output (return value)?
In this case, the inputs are two points, which you can represent using four numbers. The return value is the distance, which is a floating-point value.
Already you can write an outline of the function:
def distance(x1, y1, x2, y2):
return 0.0
Obviously, this version doesn’t compute distances; it always returns zero. But it is syntactically correct, and it runs, which means that you can test it before you make it more complicated.
To test the new function, call it with sample arguments:
>>> distance(1, 2, 4, 6)0.0
I chose these values so that the horizontal distance is 3 and the vertical distance is 4; that way, the result is 5 (the hypotenuse of a 3-4-5 triangle). When testing a function, it is useful to know the right answer.
At this point we have confirmed that the function is syntactically correct, and we can start adding code to the body. A reasonable next step is to find the differences x2 − x1 and y2 − y1. The next version stores those values in temporary variables and prints them.
def distance(x1, y1, x2, y2):
dx = x2 - x1
dy = y2 - y1
print 'dx is', dx
print 'dy is', dy
return 0.0
If the function is working, it should display 'dx is 3' and 'dy is 4' . If so, we know that the function is getting the right arguments and performing the first computation correctly. If not, there are only a few lines to check.
Next we compute the sum of squares of dx and dy:
def distance(x1, y1, x2, y2):
dx = x2 - x1
dy = y2 - y1
dsquared = dx**2 + dy**2
print 'dsquared is: ', dsquared
return 0.0
Again, you would run the program at this stage and check the output (which should be 25). Finally, you can use math.sqrt to compute and return the result:
def distance(x1, y1, x2, y2):
dx = x2 - x1
dy = y2 - y1
dsquared = dx**2 + dy**2
result = math.sqrt(dsquared)
return result
If that works correctly, you are done. Otherwise, you might want to print the value of result before the return statement.
The final version of the function doesn’t display anything when it runs; it only returns a value. The print statements we wrote are useful for debugging, but once you get the function working, you should remove them. Code like that is called scaffolding because it is helpful for building the program but is not part of the final product.
When you start out, you should add only a line or two of code at a time. As you gain more experience, you might find yourself writing and debugging bigger chunks. Either way, incremental development can save you a lot of debugging time.
The key aspects of the process are:
- Start with a working program and make small incremental changes. At any point, if there is an error, you should have a good idea where it is.
- Use temporary variables to hold intermediate values so you can display and check them.
- Once the program is working, you might want to remove some of the scaffolding or consolidate multiple statements into compound expressions, but only if it does not make the program difficult to read.
Exercise 6.2. Use incremental development to write a function called hypotenuse that returns the length of the hypotenuse of a right triangle given the lengths of the two legs as arguments. Record each stage of the development process as you go.
- 瀏覽次數:4724






