Exercises

Available under Creative Commons-NonCommercial-ShareAlike 4.0 International License.

Exercise 6.4. Draw a stack diagram for the following program. What does the program print? Solution: http://www.greenteapress.com/thinkpython/code/stack_diagram.py .

def b(z):
    prod = a(z, z)
    print z, prod
    return prod

def a(x, y):
    x = x + 1
    return x * y
def c(x, y, z):
    total = x + y + z
    square = b(total)**2
    return square

x = 1
y = x + 1
print c(x, y+3, x+y)

Exercise 6.5. The Ackermann function, A(m, n), is deﬁned:

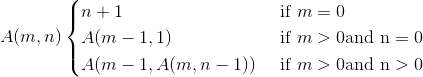
$A(m,n)\begin{cases} n+1& \text{ if } m=0 \\ A(m-1,1)& \text{ if } m> 0 \textrm{and n} = 0 \\ A(m-1,A(m,n-1))& \text{ if } m> 0\textrm{and n}> 0 \end{cases}$

See https://en.wikipedia.org/wiki/Ackermann_function. Write a function named ackthat evaluates Ackermann’s function. Use your function to evaluate ack(3, 4), which should be 125. What happens for larger values of mand n? Solution: http://thinkpython.com/code/ackermann.py.

Exercise 6.6. A palindrome is a word that is spelled the same backward and forward, like “noon” and “redivider”. Recursively, a word is a palindrome if the ﬁrst and last letters are the same and the middle is a palindrome.

The following are functions that take a string argument and return the ﬁrst, last, and middle letters:

def first(word):
    return word[0]

def last(word):
    return word[-1]

def middle(word):
    return word[1:-1]

We’ll see how they work in Strings .

Type these functions into a ﬁle named palindrome.py and test them out. What happens if you call middle with a string with two letters? One letter? What about the empty string, which is written '' and contains no letters?
Write a function called is_palindrome that takes a string argument and returns True if it is a palindrome and False otherwise. Remember that you can use the built-in function len to check the length of a string.

Solution: http://thinkpython.com/code/ paLindrome soLn.py.

Exercise 6.7. A number, a, is a power of b if it is divisible by b and a/b is a power of b. Write a function calledis_powerthat takes parameters a andb and returns Trueif a is a power of b. Note: you will have to think about the base case.

Exercise 6.8. The greatest common divisor (GCD) of a and b is the largest number that divides both of them with no remainder.

One way to ﬁnd the GCD of two numbers is based on the observation that if r is the remainder when a is divided by b, then gcd(a, b)= gcd(b, r). As a base case, we can use gcd(a,0)= a.

Write a function called gcd that takes parameters a andb and returns their greatest common divisor.

Credit: This exercise is based on an example from Abelson and Sussman’sStructure and Interpretation of Computer Programs.

瀏覽次數：2929

您在這裡

Exercises