A harmonic series can have any note as its fundamental, so there are many different harmonic series. But the relationship between the frequencies of a harmonic series is always the same. The second harmonic always has exactly half the wavelength (and twice the frequency) of the fundamental; the third harmonic always has exactly a third of the wavelength (and so three times the frequency) of the fundamental, and so on. For more discussion of wavelengths and frequencies, see Acoustics for Music Theory.
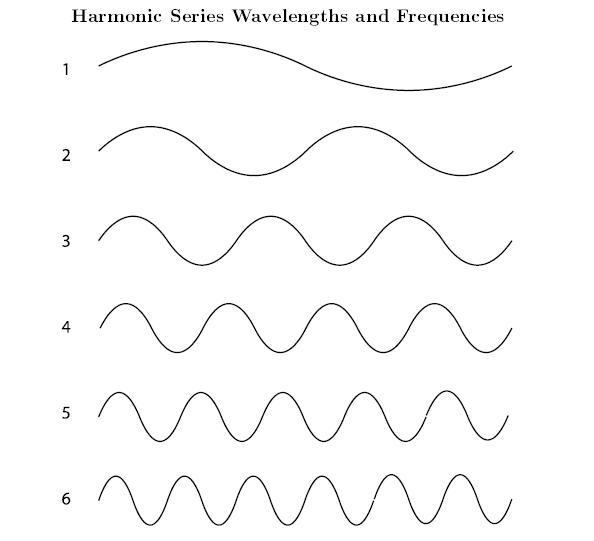
Say someone plays a note, a middle C. Now someone else plays the note that is twice the frequency of the middle C. Since this second note was already a harmonic of the first note, the sound waves of the two notes reinforce each other and sound good together. If the second person played instead the note that was just a litle bit more than twice the frequency of the first note, the harmonic series of the two notes would not fit together at all, and the two notes would not sound as good together. There are many combinations of notes that share some harmonics and make a pleasant sound together. They are considered consonant. Other combinations share fewer or no harmonics and are considered dissonant or, when they really clash, simply "out of tune" with each other. The scales and harmonies of most of the world's musics are based on these physical facts.
For example, a note that is twice the frequency of another note is one octave higher than the first note. So in the figure above, the second harmonic is one octave higher than the first; the fourth harmonic is one octave higher than the second; and the sixth harmonic is one octave higher than the third.
Exercise 3.4:
- Which harmonic will be one octave higher than the fourth harmonic?
- Predict the next four sets of octaves in a harmonic series.
- What is the pattern that predicts which notes of a harmonic series will be one octave apart?
- Notes one octave apart are given the same name. So if the first harmonic is a "A", the second and fourth will also be A's. Name three other harmonics that will also be A's.
A mathematical way to say this is "if two notes are an octave apart, the ratio of their frequencies is two to one (2:1)". Although the notes themselves can be any frequency, the 2:1 ratio is the same for all octaves. Other frequency ratios between two notes also lead to particular pitch relationships between the notes, so we will return to the harmonic series later, after learning to name those pitch relationships, or intervals.
- 5386 reads






