The Pythagorean system is so named because it was actually discussed by Pythagoras, the famous Greek mathematician and philosopher, who in the sixth century B.C. already recognized the simple arithmetical relationship involved in intervals of octaves, fifths, and fourths. He and his followers believed that numbers were the ruling principle of the universe, and that musical harmonies were a basic expression of the mathematical laws of the universe. Their model of the universe involved the "celestial spheres" making a kind of harmony as they moved in circles dictated by the same arithmetical relationships as musical harmonies.
In the Pythagorean system, all tuning is based on the interval of the pure fifth. Pure intervals are the ones found in the harmonic series, with very simple frequency ratios. So a pure fifth will have a frequency ratio of exactly 3:2. Using a series of perfect fifths (and assuming perfect octaves, too, so that you are filling in every octave as you go), you can eventually fill in an entire chromatic scale.
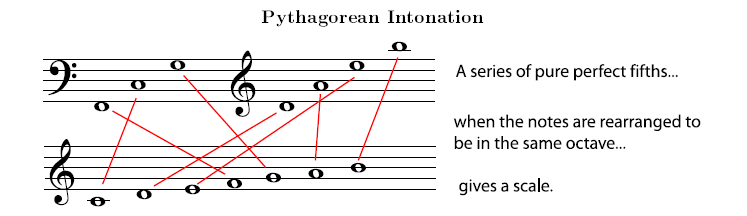
The main weakness of the Pythagorean system is that a series of pure perfect fifths will never take you to a note that is a pure octave above the note you started on. To see why this is a problem, imagine beginning on a C. A series of perfect fifths would give: C, G, D, A, E, B, F sharp, C sharp, G sharp, D sharp, A sharp, E sharp, and B sharp. In equal temperament (which doesn't use pure fifths), that B sharp would be exactly the same pitch as the C seven octaves above where you started (so that the series can, in essence, be turned into a closed loop, the The Circle of Fifths). Unfortunately, the B sharp that you arrive at after a series of pure fifths is a little higher than that C.
So in order to keep pure octaves, instruments that use Pythagorean tuning have to use eleven pure fifths and one smaller fifth . The smaller fifth has traditionally been called awolf fifth because of its unpleasant sound. Keys that avoid the wolf fifth sound just fine on instruments that are tuned this way, but keys in which the wolf fifth is often heard become a problem. To avoid some of the harshness of the wolf intervals, some harpsichords and other keyboard instruments were built with split keys for D sharp/E flat and for G sharp/A flat. The front half of the key would play one note, and the back half the other (differently tuned) note.
Pythagorean tuning was widely used in medieval and Renaissance times. Major seconds and thirds are larger in Pythagorean intonation than in equal temperament, and minor seconds and thirds are smaller. Some people feel that using such intervals in medieval music is not only more authentic, but sounds better too, since the music was composed for this tuning system.
More modern Western music, on the other hand, does not sound pleasant using Pythagorean intonation. Although the fifths sound great, the thirds (Major and Minor Intervals) are simply too far away from the pure major and minor thirds of the harmonic series. In medieval music, the third was considered a dissonance and was used sparingly - and actually, when you're using Pythagorean tuning, it really is a dissonance - but modern harmonies are built mainly on thirds (see Triads).
Some modern Non-Western music traditions, which have a very different approach to melody and harmony, still base their tuning on the perfect fifth. Wolf fifths and ugly thirds are not a problem in these traditions, which build each mode within the framework of the perfect fifth, retuning for different modes as necessary. To read a little about one such tradition, please see Indian Classical Music: Tuning and Ragas.
- 6845 reads






