If you played with the fibonacci function from One more example, you might have noticed that the bigger the argument you provide, the longer the function takes to run. Furthermore, the run time increases very quickly.
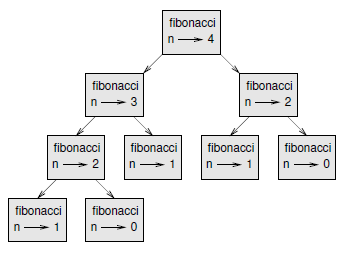
To understand why, consider Figure 11.2, which shows the call graph for fibonacci with n=4:
A call graph shows a set of function frames, with lines connecting each frame to the frames of the functions it calls. At the top of the graph, fibonacci with n=4 calls fibonacci with n=3 and n=2. In turn, fibonacci with n=3 calls fibonacci with n=2 and n=1. And so on.
Count how many times fibonacci(0) and fibonacci(1) are called. This is an inefficient solution to the problem, and it gets worse as the argument gets bigger.
One solution is to keep track of values that have already been computed by storing them in a dictionary. A previously computed value that is stored for later use is called a memo. Here is a “memoized” version of fibonacci:
known = {0:0, 1:1}
def fibonacci(n):
if n in known:
return known[n]
res = fibonacci(n-1) + fibonacci(n-2)
known[n] = res
return res
known is a dictionary that keeps track of the Fibonacci numbers we already know. It starts with two items: 0 maps to 0 and 1 maps to 1.
Whenever fibonacci is called, it checks known. If the result is already there, it can return immediately. Otherwise it has to compute the new value, add it to the dictionary, and return it.
Exercise 11.6.Run this version of fibonacci and the original with a range of parameters and compare their run times.
Exercise 11.7.Memoize the Ackermann function from Exercise 6.5 in Exercises and see if memoization makes it possible to evaluate the function with bigger arguments. Hint: no. Solution: http://thinkpython.com/code/ackermann_memo.py.
- 2792 reads






