A simple test: Do these two samples come from populations with the same variance?

Available under Creative Commons-ShareAlike 4.0 International License.

Because the F-distribution is generated by drawing two samples from the same normal population, it can be used to test the hypothesis that two samples come from populations with the same variance. You would have two samples (one of size n₁ and one of size n₂ ), and the sample variance from each. Obviously, if the two variances are very close to being equal the two samples could easily have come from populations with equal variances. Because the F-statistic is the ratio of two sample variances, when the two sample variances are close to equal, the F-score is close to one. If you compute the F-score, and it is close to one, you accept your hypothesis that the samples come from populations with the same variance.

This is the basic method of the F-test. Hypothesize that the samples come from populations with the same variance. Compute the F-score by finding the ratio of the sample variances. If the F-score is close to one, conclude that your hypothesis is correct and that the samples do come from populations with equal variances. If the F-score is far from one, then conclude that the populations probably have different variances.

The basic method must be fleshed out with some details if you are going to use this test at work. There are two sets of details: first, formally writing hypotheses, and second, using the F-distribution tables so that you can tell if your F-score is close to one or not. Formally, two hypotheses are needed for completeness. The first is the null hypothesis that there is no difference (hence "null"). It is usually denoted as H₀ :. The second is that there is a difference, and it is called the alternative, and is denoted H₁ : or H_a :.

Using the F-tables to decide how close to one is close enough to accept the null hypothesis (truly formal statisticians would say "fail to reject the null"), is fairly tricky, for the F-distribution tables are fairly tricky. Before using the tables, the researcher must decide how much chance he or she is willing to take that the null will be rejected when it is really true. The usual choice is 5 per cent, or as statisticians say, " 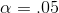". If more, or less, chance is wanted, 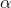can be varied. Choose your 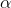and go to the F-tables. First notice that there are a number of F-tables, one for each of several different levels of 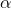(or at least a table for each two 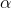's with the F-values for one 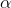in bold type and the values for the other in regular type). There are rows and columns on each F-table, and both are for degrees of freedom. Because two separate samples are taken to compute an F-score and the samples do not have to be the same size, there are two separate degrees of freedom—one for each sample. For each sample, the number of degrees of freedom is n-1, one less than the sample size. Going to the table, how do you decide which sample's degrees of freedom (df) is for the row and which is for the column? While you could put either one in either place, you can save yourself a step if you put the sample with the larger variance (not necessarily the larger sample) in the numerator, and then that sample's df determines the column and the other sample's df determines the row. The reason that this saves you a step is that the tables only show the values of F that leave α in the right tail where F > 1, the picture at the top of most F-tables shows that. Finding the critical F value for left tails requires another step, which is outlined in the box below.

F-tables are virtually always printed as "one-tail" tables, showing the critical F-value that separates the right tail from the rest of the distribution. In most statistical applications of the F-distribution, only the right tail is of interest, because most applications are testing to see if the variance from a certain source is greater than the variance from another source, so the researcher is interested in finding if the F-score is greater than one. In the test of equal variances, the researcher is interested in finding out if the F-score is close to one, so that either a large F-score or a small F-score would lead the researcher to conclude that the variances are not equal. Because the critical F-value that separates the left tail from the rest of the distribution is not printed, and not simply the negative of the printed value, researchers often simply divide the larger sample variance by the smaller sample variance, and use the printed tables to see if the quotient is "larger than one", effectively rigging the test into a one-tail format. For purists, and occasional instances, the left tail critical value can be computed fairly easily.

The left tail critical value for x, y degrees of freedom (df) is simply the inverse of the right tail (table) critical value for y, x df. Looking at an F-table, you would see that the F-value that leaves 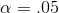in the right tail when there are 10, 20 df is F=2.35. To find the F-value that leaves 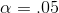in the left tail with 10, 20 df, look up F=2.77 for 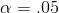, 20, 10 df. Divide one by 2.77, finding .36. That means that 5 per cent of the F-distribution for 10, 20 df is below the critical value of .36, and 5 per cent is above the critical value of 2.35.

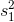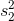Putting all of this together, here is how to conduct the test to see if two samples come from populations with the same variance. First, collect two samples and compute the sample variance of each, and . Second, write your hypotheses and choose 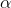. Third find the F-score from your samples, dividing the larger s² by the smaller so that F>1. Fourth, go to the tables, find the table for 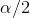, and find the critical (table) F-score for the proper degrees of freedom (n-1 and n-1). Compare it to the samples' F-score. If the samples' F is larger than the critical F, the samples' F is not "close to one", and H_a : the population variances are not equal, is the best hypothesis. If the samples' F is less than the critical F, H₀ :, that the population variances are equal should be accepted.