During an election year, we see articles in the newspaper that state confidence intervals in terms of proportions or percentages. For example, a poll for a particular candidate running for president might show that the candidate has 40% of the vote within 3 percentage points. Often, election polls are calculated with 95% confidence. So, the pollsters would be 95% confident that the true proportion of voters who favored the candidate would be between 0.37 and 0.43 : (0.40 − 0.03, 0.40 + 0.03).
Investors in the stock market are interested in the true proportion of stocks that go up and down each week. Businesses that sell personal computers are interested in the proportion of households in the United States that own personal computers. Confidence intervals can be calculated for the true proportion of stocks that go up or down each week and for the true proportion of households in the United States that own personal computers.
The procedure to find the confidence interval, the sample size, the error bound, and the confidence level for a proportion is similar to that for the population mean. The formulas are different.
How do you know you are dealing with a proportion problem? First, the underlying distribution is binomial. (There is no mention of a mean or average.) If X is a binomial random variable, then X ∼ B (n, p) where n the number of trials and p the probability of a success. To form a proportion, take X, the random variable for the number of successes and divide it by n, the number of trials (or the sample size). The random variable P' (read "P prime") is that proportion,
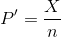
(Sometimes the random variable is denoted as 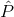 , read "P hat".)
, read "P hat".)
When n is large and p is not close to 0 or 1, we can use the normal distribution to approximate the binomial.
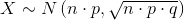
If we divide the random variable by n, the mean by n, and the standard deviation by n, we get a normal distribution of proportions with P', called the estimated proportion, as the random variable. (Recall that a proportion = the number of successes divided by n.)
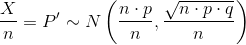
Using algebra to simplify :
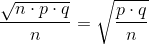
P' follows a normal distribution for proportions: 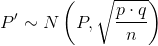
The confidence interval has the form (p' − EBP, p' + EBP).
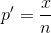
p' = the estimated proportion of successes (p' is a point estimate for p, the true proportion)
x = the number of successes.
n = the size of the sample
The error bound for a proportion is
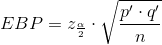
where q' = 1 - p'
This formula is similar to the error bound formula for a mean, except that the "appropriate standard deviation" is different. For a mean, when the population standard deviation is known, the
appropriate standard deviation that we use is 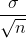 .
For a proportion, the appropriate standard deviation is
.
For a proportion, the appropriate standard deviation is 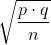 .
.
However, in the error bound formula, we use 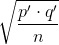 as the standard deviation, instead of
as the standard deviation, instead of 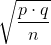 .
.
However, in the error bound formula, the standard deviation is  .
.
In the error bound formula, the sample proportions p' and q' are estimates of the unknown population proportions p and q. The estimated proportions p' and q' are used because p and q are not known. p' and q' are calculated from the data. p' is the estimated proportion of successes. q' is the estimated proportion of failures.
The confidence interval can only be used if the number of successes np' and the number of failures nq' are both larger than 5.
If 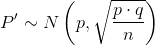 then the z-score formula is
then the z-score formula is
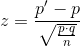
Example 4.8
Suppose that a market research firm is hired to estimate the percent of adults living in a large city who have cell phones. 500 randomly selected adult residents in this city are surveyed to
determine whether they have cell phones. Of the 500 people surveyed, 421 responded yes - they own cell phones. Using a 95% confidence level, compute a confidence interval estimate for the
true proportion of adults residents of this city who have cell phones.
Solution
- You can use technology to directly calculate the confidence interval.
- The first solution is step-by-step (Solution A).
- The second solution uses a function of the TI-83, 83+ or 84 calculators (Solution B).
Solution A
Let X = the number of people in the sample who have cell phones. X is binomial. 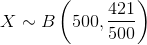 .
.
To calculate the confidence interval, you must find p', q', and EBP.
n = 500 x = the number of successes = 421
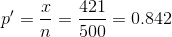
p' =0.842 is the sample proportion; this is the point estimate of the population proportion.
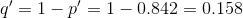
Since CL = 0.95, then α = 1 − CL = 1 − 0.95 = 0.05 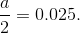 Then
Then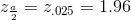
Use the TI-83, 83+ or 84+ calculator command invNorm(0.975,0,1) to find z.025. Remember that the area to the right of z.025 is 0.025 and the area to the left of
x.025 is 0.975. This can also be found using appropriate commands on other calculators, using a computer, or using a Standard Normal probability table.
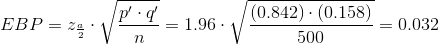
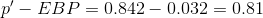
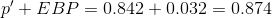
The confidence interval for the true binomial population proportion is
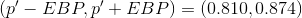
Interpretation
We estimate with 95% confidence that between 81% and 87.4% of all adult residents of this city have cell phones.
Explanation of 95% Confidence Level
95% of the confidence intervals constructed in this way would contain the true value for the population proportion of all adult residents of this city who have cell phones.
Solution B
Using a function of the TI-83, 83+ or 84 calculators:
Press STAT and arrow over to TESTS.
Arrow down toA:1-PropZint. Press ENTER.
Arrow down to x and enter 421.
Arrow down to n and enter 500.
Arrow down to C-Level and enter .95.
Arrow down to Calculate and press ENTER.
The confidence interval is (0.81003, 0.87397).
Example 4.9
For a class project, a political science student at a large university wants to estimate the percent of students that are registered voters. He surveys 500 students and finds that 300 are
registered voters. Compute a 90% confidence interval for the true percent of students that are registered voters and interpret the confidence interval.
Solution
- You can use technology to directly calculate the confidence interval.
- The first solution is step-by-step (Solution A).
- The second solution uses a function of the TI-83, 83+ or 84 calculators (Solution B).
Solution A
x = 300 and n = 500.
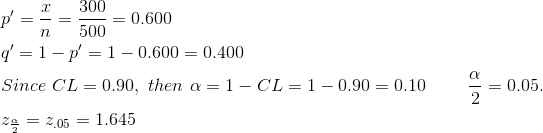 Use the TI-83, 83+ or 84+ calculator command invNorm(0.95,0,1) to find z.05.
Remember that the area to the right of z.05 is 0.05 and the area to the left of z.05 is 0.95. This can also be found using appropriate commands on other calculators, using a
computer, or using a Standard Normal probability table.
Use the TI-83, 83+ or 84+ calculator command invNorm(0.95,0,1) to find z.05.
Remember that the area to the right of z.05 is 0.05 and the area to the left of z.05 is 0.95. This can also be found using appropriate commands on other calculators, using a
computer, or using a Standard Normal probability table.
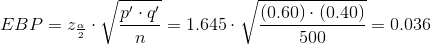
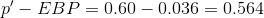
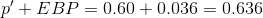
The confidence interval for the true binomial population proportion is (p' − EBP, p' + EBP) = (0.564, 0.636).
Interpretation:
- We estimate with 90% confidence that the true percent of all students that are registered voters is between 56.4% and 63.6%.
- Alternate Wording: We estimate with 90% confidence that between 56.4% and 63.6% of ALL students are registered voters.
Explanation of 90% Confidence Level
90% of all confidence intervals constructed in this way contain the true value for the population percent of students that are registered voters.
Solution B
Using a function of the TI-83, 83+ or 84 calculators:
Press STAT and arrow over to TESTS.
Arrow down to A:1-PropZint. Press ENTER.
Arrow down to x and enter 300.
Arrow down to n and enter 500.
Arrow down to C-Level and enter .90.
Arrow down to Calculate and press ENTER.
The confidence interval is (0.564, 0.636).
- 8501 reads






