Suppose X is a random variable with a distribution that may be known or unknown (it can be any distribution). Using a subscript that matches the random variable, suppose:
- µX = the mean of X
- σX = the standard deviation of X
If you draw random samples of size n, then as n increases, the random variable 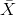 which consists of sample means, tends to be normally distributed and
which consists of sample means, tends to be normally distributed and
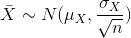
The Central Limit Theorem for Sample Means says that if you keep drawing larger and larger samples (like rolling 1, 2, 5, and, finally, 10 dice) and calculating their means the sample means form their own normal distribution (the sampling distribution). The normal distribution has the same mean as the original distribution and a variance that equals the original variance divided by n, the sample size. n is the number of values that are averaged together not the number of times the experiment is done.
To put it more formally, if you draw random samples of size n, the distribution of the random variable 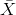 , which consists of sample means, is called the sampling distribution
of the mean. The sampling distribution of the mean approaches a normal distribution as n, the sample size, increases.
, which consists of sample means, is called the sampling distribution
of the mean. The sampling distribution of the mean approaches a normal distribution as n, the sample size, increases.
The random variable 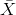 has a different z-score associated with it
than the random variable X.
has a different z-score associated with it
than the random variable X. 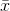 is
the value of
is
the value of 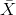 in one sample.
in one sample.
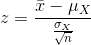
µX is both the average of X and of 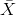 .
.
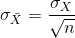 = standard deviation
of
= standard deviation
of 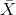 and is called the standard error of
the mean.
and is called the standard error of
the mean.
Example 3.7
An unknown distribution has a mean of 90 and a standard deviation of 15. Samples of size n = 25 are drawn randomly from the population.
See Problem 1-2.
Problem 1
Find the probability that the sample mean is between 85 and 92.
Solution
Let X = one value from the original unknown population. The probability question asks you to find a probability for the sample mean.
Let 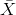 = the mean of a sample of size 25. Since µX = 90,
σX = 15, and n = 25;
= the mean of a sample of size 25. Since µX = 90,
σX = 15, and n = 25;
then 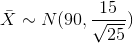
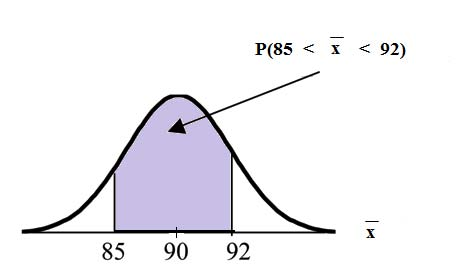
Find P (85 <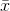 < 92) Draw a graph.
< 92) Draw a graph.
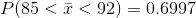
The probability that the sample mean is between 85 and 92 is 0.6997.
TI-83 or 84: normalcdf(lower value, upper value, mean, standard error of the mean)
The parameter list is abbreviated (lower value, upper value, µ, 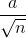 )
)
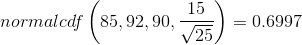
Problem 2
Find the value that is 2 standard deviations above the expected value (it is 90) of the sample mean.
Solution
To find the value that is 2 standard deviations above the expected value 90, use the formula

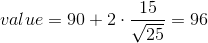
So, the value that is 2 standard deviations above the expected value is 96.
Example 3.8
The length of time, in hours, it takes an "over 40" group of people to play one soccer match is normally distributed with a mean of 2 hours and a standard deviation of 0.5 hours. A sample of size n = 50 is drawn randomly from the population.
See Problem below.
Problem
Find the probability that the sample mean is between 1.8 hours and 2.3 hours.
Solution
Let X = the time, in hours, it takes to play one soccer match.
The probability question asks you to find a probability for the sample mean time, in hours, it takes to play one soccer
match.
Let 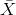 the mean time , in hours, it
takes to play one soccer match.
the mean time , in hours, it
takes to play one soccer match.
If µX = ________ , σX = ________ , and n = ________ , then 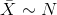 (________, ________) by the Central Limit Theorem for Means.
(________, ________) by the Central Limit Theorem for Means.
µX = 2, σX = 0.5, n = 50, and 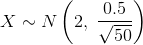
Find 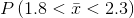 . Draw a graph.
. Draw a graph.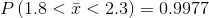
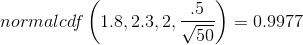
The probability that the mean time is between 1.8 hours and 2.3 hours is ________.
- 4138 reads






