If researchers desire a specific margin of error, then they can use the error bound formula to calculate the required sample size. The error bound formula for a population proportion is
-
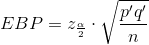
- Solving for n gives you an equation for the sample size.
-
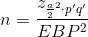
Example 4.10
Suppose a mobile phone company wants to determine the current percentage of customers aged 50+ that use text messaging on their cell phone. How many customers aged 50+ should the company
survey in order to be 90% confident that the estimated (sample) proportion is within 3 percentage points of the true population proportion of customers aged 50+ that use text messaging on
their cell phone.
Solution
From the problem, we know that EBP=0.03 (3% 0.03) and
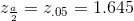 because the confidence level is 90%
because the confidence level is 90%
However, in order to find n , we need to know the estimated (sample) proportion p'. Remember that q' = 1-p'. But, we do not know p' yet. Since we multiply p' and q' together, we make them
both equal to 0.5 because p'q' = (.5)(.5) = .25 results in the largest possible product. (Try other products: (.6)(.4) = .24; (.3)(.7) = .21; (.2)(.8) = .16 and so on). The largest possible
product gives us the largest n. This gives us a large enough sample so that we can be 90% confident that we are within 3 percentage points of the true population proportion. To calculate the
sample size n, use the formula and make the substitutions.
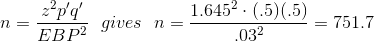
Round the answer to the next higher value. The sample size should be 752 cell phone customers aged 50+ in order to be 90% confident that the estimated (sample) proportion is within 3
percentage points of the true population proportion of all customers aged 50+ that use text messaging on their cell phone.
**With contributions from Roberta Bloom.
- 3549 reads






