Use the sample data to calculate the actual probability of getting the test result, called the p-value. The p-value is the probability that, if the null hypothesis is true, the results from another randomly selected sample will be as extreme or more extreme as the results obtained from the given sample.
A large p-value calculated from the data indicates that we should fail to reject the null hypothesis. The smaller the p-value, the more unlikely the outcome, and the stronger the evidence is against the null hypothesis. We would reject the null hypothesis if the evidence is strongly against it.
Draw a graph that shows the p-value. The hypothesis test is easier to perform if you use a graph because you see the problem more clearly.
Example 5.5: (to illustrate the p-value)
Suppose a baker claims that his bread height is more than 15 cm, on the average. Several of his customers do not believe him. To persuade his customers that he is right, the baker decides to
do a hypothesis test. He bakes 10 loaves of bread. The mean height of the sample loaves is 17 cm. The baker knows from baking hundreds of loaves of bread that the standard deviation for the height is 0.5 cm. and the distribution of heights is normal.
The null hypothesis could be Ho: µ ≤ 15
The alternate hypothesis is Ha: µ> 15
The words "is more than" translates as a ">" so "µ> 15" goes into the alternate hypothesis. The null hypothesis must contradict the alternate
hypothesis.
Since σ is known (σ =0.5 cm.), the distribution for the population is known to be normal with mean µ= 15 and standard deviation 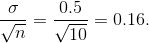
Suppose the null hypothesis is true (the mean height of the loaves is no more than 15 cm). Then is the mean height (17 cm) calculated from the sample unexpectedly large? The hypothesis test
works by asking the question how unlikely the sample mean would be if the null hypothesis were true. The graph shows how far out the sample mean is on the normal
curve. The p-value is the probability that, if we were to take other samples, any other sample mean would fall at least as far out as 17 cm.
The p-value, then, is the probability that a sample mean is the same or greater than 17 cm. when the population mean is, in fact, 15 cm. We can calculate this
probability using the normal distribution for means from Chapter 7.
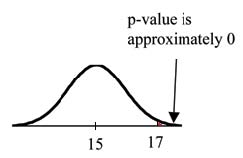
p-value = P (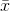 > 17) which is approximately 0.
> 17) which is approximately 0.
A p-value of approximately 0 tells us that it is highly unlikely that a loaf of bread rises no more than 15 cm, on the average. That is, almost 0% of all loaves of bread would be at least as
high as 17 cm. purely by CHANCE had the population mean height really been 15 cm. Because the outcome of 17 cm. is so unlikely (meaning it
is happening NOT by chance alone), we conclude that the evidence is strongly against the null hypothesis (the mean height is at most 15 cm.). There is sufcient evidence that the true
mean height for the population of the baker's loaves of bread is greater than 15 cm.
- 4904 reads






