If researchers desire a specifc margin of error, then they can use the error bound formula to calculate the required sample size.
The error bound formula for a population mean when the population standard deviation is known is
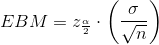
The formula for sample size is 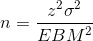 , found
by solving the error bound formula for n
, found
by solving the error bound formula for n
In this formula, z is  , corresponding to the desired
confidence level. A researcher planning a study who 2 wants a specifed confidence level and error bound can use this formula to calculate the size of the sample needed for the study.
, corresponding to the desired
confidence level. A researcher planning a study who 2 wants a specifed confidence level and error bound can use this formula to calculate the size of the sample needed for the study.
Example 4.6
The population standard deviation for the age of Foothill College students is 15 years. If we want to be 95% confident that the sample mean age is within 2 years of the true population mean
age of Foothill College students , how many randomly selected Foothill College students must be surveyed?
From the problem, we know that σ = 15 and EBM = 2
z = z.025 = 1.96, becuase the confidence level is 95%.
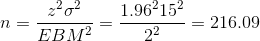
using the sample size equation.
Use n = 217: Always round the answer UP to the next higher integer to ensure that the sample size is large enough.
Therefore, 217 Foothill College students should be surveyed in order to be 95% confident that we are within 2 years of the true population mean age of Foothill College students.
**With contributions from Roberta Bloom
- 3587 reads






