Twenty students were asked how many hours they worked per day. Their responses, in hours, are listed below:
5; 6; 3; 3; 2; 4; 7; 5; 2; 3; 5; 6; 5; 4; 4; 3; 5; 2; 5; 3
Below is a frequency table listing the different data values in ascending order and their frequencies.
|
DATA VALUE |
FREQUENCY |
|---|---|
|
2 |
3 |
|
3 |
5 |
|
4 |
3 |
|
5 |
6 |
|
6 |
2 |
|
7 |
1 |
A frequency is the number of times a given datum occurs in a data set. According to the table above, there are three students who work 2 hours, five students who work 3 hours, etc. The total of the frequency column, 20, represents the total number of students included in the sample.
A relative frequency is the fraction or proportion of times an answer occurs. To find the relative frequencies, divide each frequency by the total number of students in the sample - in this case, 20. Relative frequencies can be written as fractions, percents, or decimals.
|
DATA VALUE |
FREQUENCY |
RELATIVE FREQUENCY |
|---|---|---|
|
2 |
3 |
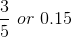
|
| 3 | 5 |
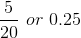
|
| 4 | 3 |
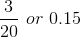
|
| 5 | 6 |
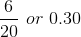
|
| 6 | 2 |
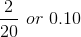
|
| 7 | 1 |
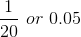
|
The sum of the relative frequency column is 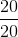 or 1.
or 1.
Cumulative relative frequency is the accumulation of the previous relative frequencies. To find the cumulative relative frequencies, add all the previous relative frequencies to the relative frequency for the current row.
|
DATA VALUE |
FREQUENCY |
RELATIVE FREQUENCY | CUMULATIVE RELATIVE FREQUENCY |
|---|---|---|---|
|
2 |
3 |
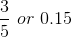
|
0.15 |
| 3 | 5 |

|
0.15+0.25=0.40 |
| 4 | 3 |
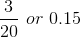
|
0.40+0.15=0.55 |
| 5 | 6 |
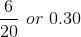
|
0.55+0.30=0.85 |
| 6 | 2 |
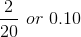
|
0.85+0.10=0.95 |
| 7 | 1 |
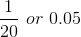
|
0.95+0.05=1.00 |
The last entry of the cumulative relative frequency column is one, indicating that one hundred percent of the data has been accumulated.
The following table represents the heights, in inches, of a sample of 100 male semiprofessional soccer players.
|
HEIGHT (INCHES) |
FREQUENCY |
RELATIVE FREQUENCY | CUMULATIVE RELATIVE FREQUENCY |
|---|---|---|---|
| 59.95 - 61.95 | 5 |
|
0.05 |
| 61.95 - 63.95 | 3 |
|
0.05+0.03=0.08 |
| 63.95 - 65.95 | 15 |
|
0.08+0.15=0.23 |
| 65.95 - 67.95 | 40 |
|
0.23+0.40=0.63 |
| 67.95 - 69.95 | 17 |
|
0.63+0.17=0.80 |
| 69.95 - 71.95 | 12 |
|
0.80+0.12=0.92 |
| 71.95 - 73.95 | 7 |
|
0.92+0.07=0.99 |
| 73.95 - 75.95 | 1 |
|
0.99+0.01=1.00 |
| Total = 100 | Total = 1.00 |
The data in this table has been grouped into the following intervals:
- 59.95 - 61.95 inches
- 61.95 - 63.95 inches
- 63.95 - 65.95 inches
- 65.95 - 67.95 inches
- 67.95 - 69.95 inches
- 69.95 - 71.95 inches
- 71.95 - 73.95 inches
- 73.95 - 75.95 inches
In this sample, there are 5 players whose heights are between 59.95 - 61.95 inches, 3 players whose heights fall within the interval 61.95 - 63.95 inches, 15 players whose heights fall within the interval 63.95 - 65.95 inches, 40 players whose heights fall within the interval 65.95 - 67.95 inches, 17 players whose heights fall within the interval 67.95 - 69.95 inches, 12 players whose heights fall within the interval 69.95 - 71.95, 7 players whose height falls within the interval 71.95 - 73.95, and 1 player whose height falls within the interval 73.95 - 75.95. All heights fall between the endpoints of an interval and not at the endpoints.
Example 1.6
From the table, find the percentage of heights that are less than 65.95 inches.
Solution
If you look at the first, second, and third rows, the heights are all less than 65.95 inches. There are 5 + 3 + 15 = 23 males whose heights are less than 65.95 inches. The percentage of
heights less than 65.95 inches is then 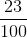 or 23%. This
percentage is the cumulative relative frequency entry in the third row.
or 23%. This
percentage is the cumulative relative frequency entry in the third row.
Example 1.7
From the table, find the percentage of heights that fall between 61.95 and 65.95 inches.
Solution
Add the relative frequencies in the second and third rows: 0.03 + 0.15 = 0.18 or 18%.
Example 1.8
Use the table of heights of the 100 male semiprofessional soccer players. Fill in the blanks and check your answers.
- The percentage of heights that are from 67.95 to 71.95 inches is:
- The percentage of heights that are from 67.95 to 73.95 inches is:
- The percentage of heights that are more than 65.95 inches is:
- The number of players in the sample who are between 61.95 and 71.95 inches tall is:
- What kind of data are the heights?
- Describe how you could gather this data (the heights) so that the data are characteristic of all male semiprofessional soccer players.
Remember, you count frequencies. To find the relative frequency, divide the frequency by the total number of data values. To find the cumulative relative frequency, add all of the previous relative frequencies to the relative frequency for the current row.
- 瀏覽次數:154103






