您在這裡

首頁 » Principles of Business Statistics » Linear Regression and Correlation » Linear Regression and Correlation: Correlation Coefficient and Coefficient of Determination

The Correlation Coefficient r

26 七月, 2019 - 12:02
Available under Creative Commons-ShareAlike 4.0 International License. Download for free at http://cnx.org/contents/733d1554-5d75-4798-9e54-7dcdc1ee5690@5.40

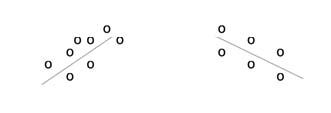
Besides looking at the scatter plot and seeing that a line seems reasonable, how can you tell if the line is a good predictor? Use the correlation coefficient as another indicator (besides the scatterplot) of the strength of the relationship between x and y.

The correlation coefficient, r, developed by Karl Pearson in the early 1900s, is a numerical measure of the strength of association between the independent variable x and the dependent variable y.
The correlation coefficient is calculated as

r=\frac{n\cdot \sum x\cdot y-(\sum x)\cdot(\sum y)}{\sqrt{[n\cdot \sum x^{2}-(\sum x)^{2}]\cdot[n\cdot\sum y^{2}-(\sum y)^{2}]}}

where n = the number of data points.

If you suspect a linear relationship between x and y, then r can measure how strong the linear relationship is.

What the VALUE of r tells us:

  • The value of r is always between -1 and +1: −1 ≤ r ≤ 1.
  • The size of the correlation r indicates the strength of the linear relationship between x and y. Values of r close to -1 or to +1 indicate a stronger linear relationship between x and y.
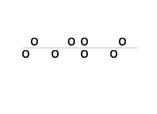
  • If r = 0 there is absolutely no linear relationship between x and y (no linear correlation).
  • If r = 1, there is perfect positive correlation. If r = −1, there is perfect negative correlation. In both these cases, all of the original data points lie on a straight line. Of course, in the real world, this will not generally happen.

What the SIGN of r tells us

  • A positive value of r means that when x increases, y tends to increase and when x decreases, y tends to decrease (positive correlation).
  • A negative value of r means that when x increases, y tends to decrease and when x decreases, y tends to increase (negative correlation).
  • The sign of r is the same as the sign of the slope, b, of the best fit line.
Note: Strong correlation does not suggest that x causes y or y causes x. We say "correlation does not imply causation." For example, every person who learned math in the 17th century is dead. However, learning math does not necessarily cause death!
media/image201.png
Figure 6.11 (a) A scatter plot showing data with a positive correlation. 0 <r< 1 (b) A scatter plot showing data with a negative correlation. −1 <r< 0  
 
media/image202.png
Figure 6.12 (C) A scatter plot showing data with zero correlation. r=0  

The formula for r looks formidable. However, computer spreadsheets, statistical software, and many calculators can quickly calculate r. The correlation coefficient r is the bottom item in the output screens for the LinRegTTest on the TI-83, TI-83+, or TI-84+ calculator (see previous section for instructions).

  • 瀏覽次數：2170