A corporation must decide whether to introduce a new product line. The new product will have startup costs, operational costs, and incoming cash flows over six years. This project will have an immediate (t=0) cash outflow of $100,000 (which might include machinery, and employee training costs). Other cash outflows for years 1-6 are expected to be $5,000 per year. Cash inflows are expected to be $30,000 each for years 1-6. All cash flows are after-tax, and there are no cash flows expected after year 6. The required rate of return is 10%. The present value (PV) can be calculated for each year:
| Year | Cashflow | Present Value |
|---|---|---|
| T=0 |
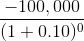
|
-$100,000 |
| T=1 |
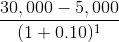
|
$22,727 |
| T=2 |
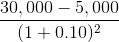
|
$20,661 |
| T=3 |
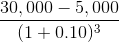
|
$18,783 |
| T=4 |
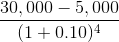
|
$17,075 |
| T=5 |
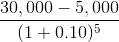
|
$15,523 |
| T=6 |
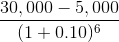
|
$14,112 |
The sum of all these present values is the net present value, which equals $8,881.52. Since the NPV is greater than zero, it would be better to invest in the project than to do nothing, and the corporation should invest in this project if there is no alternative with a higher NPV.
More realistic problems would need to consider other factors, generally including the calculation of taxes, uneven cash flows, and salvage values as well as the availability of alternate investment opportunities.
- 2387 reads






