MPT assumes that investors are risk averse, meaning that given two portfolios that offer the same expected return, investors will prefer the less risky one. Thus, an investor will take on increased risk only if compensated by higher expected returns. Conversely, an investor who wants higher expected returns must accept more risk. The exact trade-off will be the same for all investors, but different investors will evaluate the trade-off differently based on individual risk aversion characteristics. The implication is that a rational investor will not invest in a portfolio if a second portfolio exists with a more favorable risk-expected return profile – i.e., if for that level of risk an alternative portfolio exists which has better expected returns.
Note that the theory uses standard deviation of return as a proxy for risk, which is valid if asset returns are jointly normally distributed or otherwise elliptically distributed. There are problems with this, however; see criticism.
Under the model:
- Portfolio return is the proportion-weighted combination of the constituent assets' returns.
- Portfolio volatility is a function of the correlations ρij of the component assets, for all asset pairs (i, j).
In general:
Expected return:
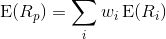
where 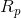 is the return on the portfolio,
is the return on the portfolio, 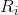 is the return on asset i and
is the return on asset i and 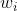 is the weighting of component asset
is the weighting of component asset 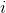 (that is, the share of asset i in the portfolio).
(that is, the share of asset i in the portfolio).
Portfolio return variance:
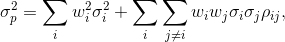
where 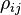 is the correlation coefficient between the returns on assets i and j.
Alternatively the expression can be written as:
is the correlation coefficient between the returns on assets i and j.
Alternatively the expression can be written as:
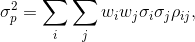
where 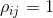 for i=j.
for i=j.
Portfolio return volatility (standard deviation):
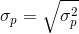
For a two asset portfolio:
Portfolio return: 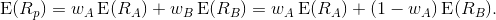
Portfolio variance: 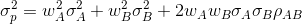
For a three asset portfolio:
Portfolio return: 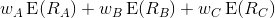
Portfolio variance: 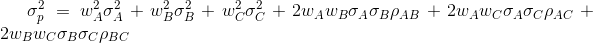
- 2092 reads






