Risky asset returns are said to follow a factor structure if they can be expressed as:
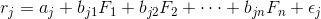
where
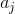 is a constant for asset j
is a constant for asset j
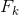 is a systematic factor
is a systematic factor
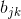 is the sensitivity of the jth asset to factor
is the sensitivity of the jth asset to factor 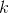 , also called factor loading,
, also called factor loading,
and 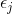 is the risky asset's idiosyncratic random shock with mean zero.
is the risky asset's idiosyncratic random shock with mean zero.
Idiosyncratic shocks are assumed to be uncorrelated across assets and uncorrelated with the factors.
The APT states that if asset returns follow a factor structure then the following relation exists between expected returns and the factor sensitivities:
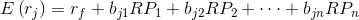
where
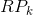 is the risk premium of the factor,
is the risk premium of the factor,
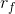 is the risk-free rate,
is the risk-free rate,
That is, the expected return of an asset j is a linear function of the assets sensitivities to the n factors.
Note that there are some assumptions and requirements that have to be fulfilled for the latter to be correct: There must be perfect competition in the market, and the total number of factors may never surpass the total number of assets (in order to avoid the problem of matrix singularity),
- 2121 reads






