Imagine that the health psychologist now knows that people tend to underestimate the number of calories in junk food and has developed a short training program to improve their estimates. To test the effectiveness of this program, he conducts a pretest-posttest study in which 10 participants estimate the number of calories in a chocolate chip cookie before the training program and then again afterward. Because he expects the program to increase the participants’ estimates, he decides to do a one-tailed test. Now imagine further that the pretest estimates are
230, 250, 280, 175, 150, 200, 180, 210, 220, 190
and that the posttest estimates (for the same participants in the same order) are
250, 260, 250, 200, 160, 200, 200, 180, 230, 240.
The difference scores, then, are as follows:
+20, +10, −30, +25, +10, 0, +20, −30, +10, +50.
Note that it does not matter whether the first set of scores is subtracted from the second or the second from the first as long as it is done the same way for all participants. In this example, it makes sense to subtract the pretest estimates from the posttest estimates so that positive difference scores mean that the estimates went up after the training and negative difference scores mean the estimates went down.
The mean of the difference scores is 8.50 with a standard deviation of 27.27. The health psychologist can now compute the tscore for his sample as follows:
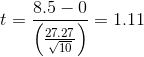
If he enters the data into one of the online analysis tools or uses Excel or SPSS, it would tell him that the one-tailed p value for this t score (again with 10 − 1 = 9 degrees of freedom) is .148. Because this is greater than .05, he would retain the null hypothesis and conclude that the training program does not increase people’s calorie estimates. If he were to compute the t score by hand, he could look at Table 13.2 and see that the critical value of t for a one-tailed test with 9 degrees of freedom is +1.833. (It is positive this time because he was expecting a positive mean difference score.) The fact that his t score was less extreme than this critical value would tell him that his p value is greater than .05 and that he should fail to reject the null hypothesis.
- 2931 reads






