In Corporate Finance, it is often necessary to determine if a project is worthwhile to undertake. Sometimes, there will only be enough investment capital to undertake some projects, in which case, one must determine which project to do.
The standard approach is to use the Net Present Value, or NPV. The NPV is calculated by finding all of the cash flows which will occur, and discount them back to the present time. This also includes expenses, hence, net present value.
For example:
STDs Unlimited is trying to determine whether to purchase a new piece of machinery. This machine will cost $1,000,000, and save $170,000 per year for 10 years, at which point it will be sold for $50,000. After 5 years, the machine will require an overhaul which will cost $100,000. If the company uses a 7% discount rate for projects of this type, what is the NPV of purchasing the machine? Should the company do it?
The first thing we must do is find the total cost savings of this project. Each year there will be a positive cash flow of $170,000, which must be discounted each year back to the present time:
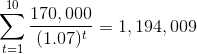
So we can see that this project will bring in $1,194,009 worth of savings. In addition, it will bring in $50,000 in year 10 when it is sold, so we find the present value of that:
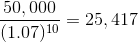
So we add those up to get the total positive cash flow of $1,219,426.
From this amount, we must subtract the costs. We know the initially cash outlay is $1,000,000, but we must find the present value of the overhaul which will occur at year 5:
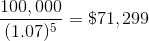
So now we can calculate the present value of all costs: 1,000,000 + 71,299 = 1,071,299.
Then we simply subtract the negative cash flows from the positive and see that
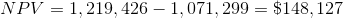
So, since this project has a positive NPV, the company should go ahead and do it.
- 1840 reads






