In the previous example, we did not calculate an important benefit which must be considered in real life examples: taxes. When a company purchases a piece of equipment, they will depreciate it. This means that they do not have to pay taxes on an amount of income equivalent to what they are spending on capital investment.
Let's consider our example above. We arrived at the NPV of $148,127 without taxes, so lets look at what happens when we depreciate the initial investment:
Assume STDs unlimited decides to depreciate the $1,000,000 machine using straight line depreciation for 10 years. What is the value of the depreciation tax shield? What is the new NPV?
Straight line depreciation means an equivalent amount is depreciated each year, for 10 years. So in this example, depreciation is $100,000 per year. This means that on the books, the company will spend $100,000 per year on the machine, instead of $1,000,000 up front. This makes more sense logically, since the company will be using the machine for 10 full years. The tax shield is equal to the following:
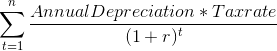
In this case it will be:
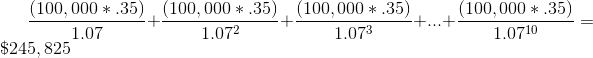
As we can see, this is a significant savings.
There is one more step we must take in this example. Since we depreciated the entire value of the machine, we are basically telling the government that it is worthless at the end of 10 years. However, since we sell at at the end of year 10 for $50,000, it is clearly not worthless. In order to make this right (and avoid an audit and costly fines), we must pay taxes on that $50,000 in year 10. This amount is clearly .35 * 50,000 = 17,500. Since we don't pay this until year 10, we discount this amount by ten years (17,500/(1.07^10)) to get $8,896. We then subtract this amount from the $245,825 tax shield to get $236,929.
So we see that our total tax savings from depreciation is $236,929, which we add to our NPV of 148,127 to get a final NPV on this project of $385,056.
- 2550 reads






