When a company is considering two machines which will be used for a long period of time, it is sometimes necessary to use equivalent annual costs to determine which machine is a better investment.
For example:
Suppose an upscale vodka company is looking to purchase one of the two distilling machines. Machine A costs $45,000, lasts for 5 years before replacement, and costs $10,000 per year to operate. Machine B costs $50,000, lasts for 7 years, and costs $11,000 per year to operate. Now, if we were to take the NPV of the costs, it looks quite obvious that machine B's NPV will be lower (meaning it costs more). We shall use an 8% discount rate.
NPVA=-$84,927
NPVB=-$107,270
Now, if we were to just look at NPV, we would choose machine A, as it has lower costs. However, this fails to take into account that machine B has to be replaced less often. In order to correctly evaluate these options, we must use Equivalent Annual Cost.
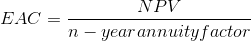
An annuity factor is defined as the present value of $1 received every year for n years, at a discount rate of r.The formula to find the n-year annuity factor is as follows:
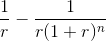
Using this formula, we can see that the 5 year annuity factor at 8% is 3.99, and the 7 year annuity factor is 5.2.
So, in order to find the equivalent annual costs of these projects, we shall divide their respective NPVs by their respective annuity factors:
| Machine A | Machine B |
|---|---|
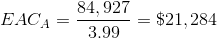
|
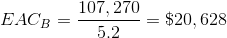
|
And so, we can see that although machine A appears to have lower costs, machine B is actually cheaper in the long run, since it must be replaced less frequently.
- 2342 reads






