We assume that each consumer seeks the highest indifference curve possible. The budget line gives the combinations of two goods that the consumer can purchase with a given budget. Utility maximization is therefore a matter of selecting a combination of two goods that satisfies two conditions:
- The point at which utility is maximized must be within the attainable region defined by the budget line.
- The point at which utility is maximized must be on the highest indifference curve consistent with condition 1.
Figure 7.11 combines Janet Bain’s budget line from Figure 7.7 with her indifference curves from Figure 7.9. Our two conditions for utility maximization are satisfied at point X, where she skis 2 days per semester and spends 3 days horseback riding.
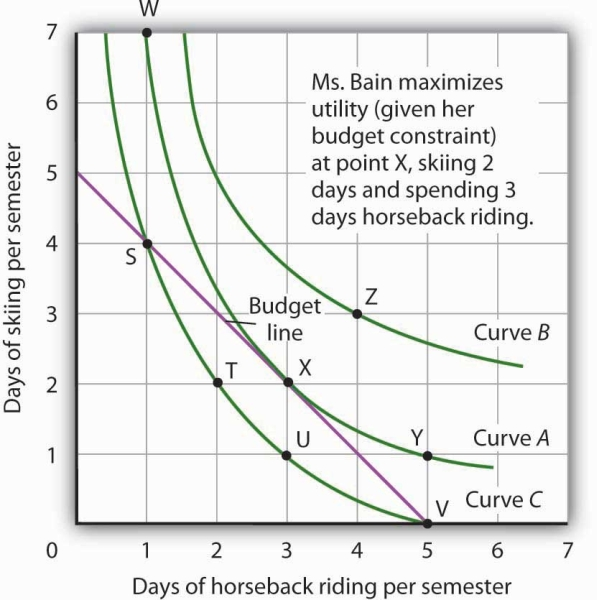
Combining Janet Bain’s budget line and indifference curves from Figure 7.7 and Figure 7.9, we find a point that (1) satisfies the budget constraint and (2) is on the highest indifference curve possible. That occurs for Ms. Bain at point X.
The highest indifference curve possible for a given budget line is tangent to the line; the indifference curve and budget line have the same slope at that point. The absolute value of the slope of the indifference curve shows theMRSbetween two goods. The absolute value of the slope of the budget line gives the price ratio between the two goods; it is the rate at which one good exchanges for another in the market. At the point of utility maximization, then, the rate at which the consumer is willing to exchange one good for another equals the rate at which the goods can be exchanged in the market. For any two goods X and Y, with good X on the horizontal axis and good Y on the vertical axis,
| MRSX,Y=PXPY |
- 瀏覽次數:3792






