Suppose a local district attorney (DA) is certain that two individuals, Frankie and Johnny, have committed a burglary, but she has no evidence that would be admissible in court.
The DA arrests the two. On being searched, each is discovered to have a small amount of cocaine. The DA now has a sure conviction on a possession of cocaine charge, but she will get a conviction on the burglary charge only if at least one of the prisoners confesses and implicates the other.
The DA decides on a strategy designed to elicit confessions. She separates the two prisoners and then offers each the following deal: “If you confess and your partner doesn’t, you will get the minimum sentence of one year in jail on the possession and burglary charges. If you both confess, your sentence will be three years in jail. If your partner confesses and you do not, the plea bargain is off and you will get six years in prison. If neither of you confesses, you will each get two years in prison on the drug charge.”
The two prisoners each face a dilemma; they can choose to confess or not confess. Because the prisoners are separated, they cannot plot a joint strategy. Each must make a strategic choice in isolation.
The outcomes of these strategic choices, as outlined by the DA, depend on the strategic choice made by the other prisoner. The payoff matrix for this game is given in Figure 11.4. The two rows represent Frankie’s strategic choices; she may confess or not confess. The two columns represent Johnny’s strategic choices; he may confess or not confess. There are four possible outcomes: Frankie and Johnny both confess (cell A), Frankie confesses but Johnny does not (cell B), Frankie does not confess but Johnny does (cell C), and neither Frankie nor Johnny confesses (cell D). The portion at the lower left in each cell shows Frankie’s payoff; the shaded portion at the upper right shows Johnny’s payoff.
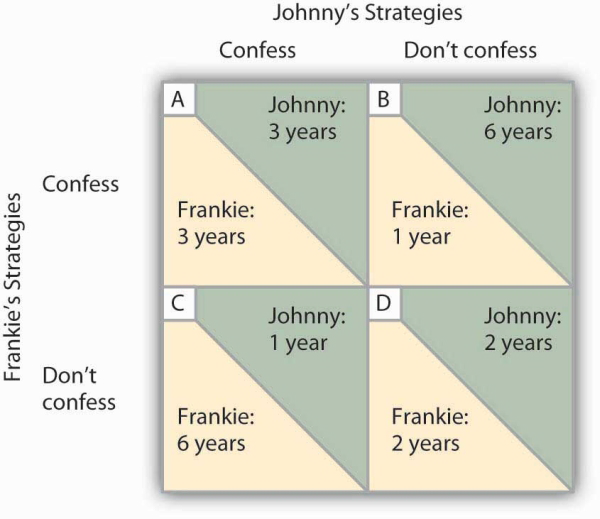
The four cells represent each of the possible outcomes of the prisoners’ game.
If Johnny confesses, Frankie’s best choice is to confess—she will get a three-year sentence rather than the six-year sentence she would get if she did not confess. If Johnny does not confess, Frankie’s best strategy is still to confess—she will get a one-year rather than a two-year sentence. In this game, Frankie’s best strategy is to confess, regardless of what Johnny does. When a player’s best strategy is the same regardless of the action of the other player, that strategy is said to be a dominant strategy. Frankie’s dominant strategy is to confess to the burglary.
For Johnny, the best strategy to follow, if Frankie confesses, is to confess. The best strategy to follow if Frankie does not confess is also to confess. Confessing is a dominant strategy for Johnny as well. A game in which there is a dominant strategy for each player is called a dominant strategy equilibrium. Here, the dominant strategy equilibrium is for both prisoners to confess; the payoff will be given by cell A in the payoff matrix.
From the point of view of the two prisoners together, a payoff in cell D would have been preferable. Had they both denied participation in the robbery, their combined sentence would have been four years in prison—two years each. Indeed, cell D offers the lowest combined prison time of any of the outcomes in the payoff matrix. But because the prisoners cannot communicate, each is likely to make a strategic choice that results in a more costly outcome. Of course, the outcome of the game depends on the way the payoff matrix is structured.
- 瀏覽次數:2810






